Project Alumni: Shawna Thomas, Chinwe Ekenna
Supported By: NSF, Schlumberger Faculty for the Future Fellowship
Probabilistic Roadmap Methods (PRMs) solve the motion planning problem in two phases by sampling free configurations and connecting them together to build a map that is used to find a valid path. Existing algorithms are highly sensitive to the topology of the problem, and their efficiency depends on applying them to a compatible problem. Reinforcement learning has been applied to motion planning and rewards the action performed by planners during either sampling or connection.
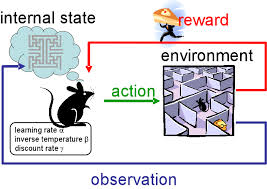
Reinforcement Learning Example |
In this work we use machine learning techniques to intelligently combine and use any existing PRM method. This affords us the opportunity to use all available PRM method irrespective of the problem scenario. We show in our experiments that we are able to remove the overhead of deciding what PRM method to use for a given input problem. We test on a variety of heterogeneous environment including protein folding simulations and we utilize the strengths (ability to generate samples in narrow passages) of these methods when needed while minimizing their weaknesses (time needed to solve a query).
Heterogenous Environment Example |
Probabilistic Roadmap Methods (PRMs) are widely used motion planning methods that sample robot configurations (nodes) and connect them to form a graph (roadmap) containing feasible trajectories. Many PRM variants propose different strategies for each of the steps and choosing among them is problem dependent. Planning in heterogeneous environments and/or on parallel machines necessitates dividing the problem into regions where these choices have to be made for each one. Hand-selecting the best method for each region becomes infeasible. In particular, there are many ways to select connection candidates, and choosing the appropriate strategy is input dependent.
In this work, we present a general connection framework that adaptively selects a neighbor finding strategy from a candidate set of options. Our framework learns which strategy to use by examining their success rates and costs. It frees the user of the burden of selecting the best strategy and allows the selection to change over time.
We perform experiments on rigid bodies of varying geometry and articulated linkages up to 37 degrees of freedom. Our results show that strategy performance is indeed problem/region dependent, and our adaptive method harnesses their strengths. Over all problems studied, our method differs the least from manual selection of the best method, and if one were to manually select a single method across all problems, the performance can be quite poor. Our method is able to adapt to changing sampling density and learns different strategies for each region when the problem is partitioned for parallelism.
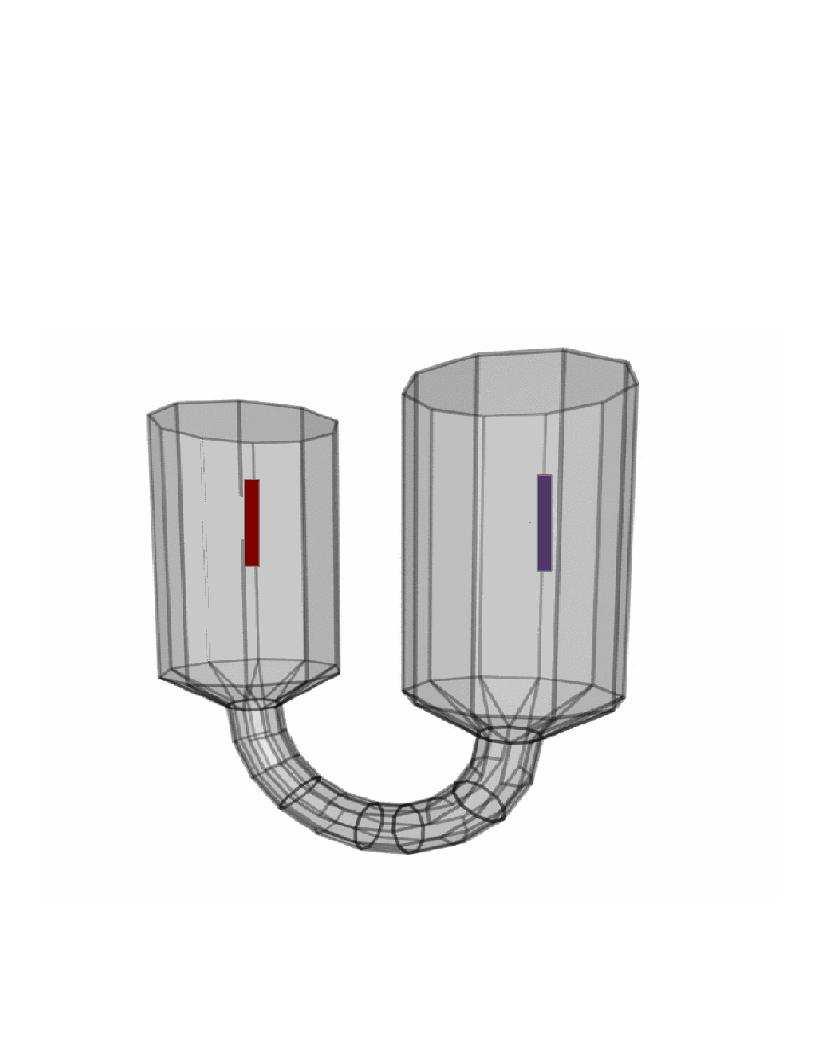
U-Tunnel Environment |
Maze Heterogenous Environment |
The U-tunnel environment has a long rigid body robot which behaves much differently than the compact robots in the prior environments. Here, ANC performs significantly better than the other methods in terms of running time and roadmap size and near the best in terms of Edges/Nodes ratio. Figure 3 provides the learning plot. Again, ANC is able to adapt and learn a good connection strategy.
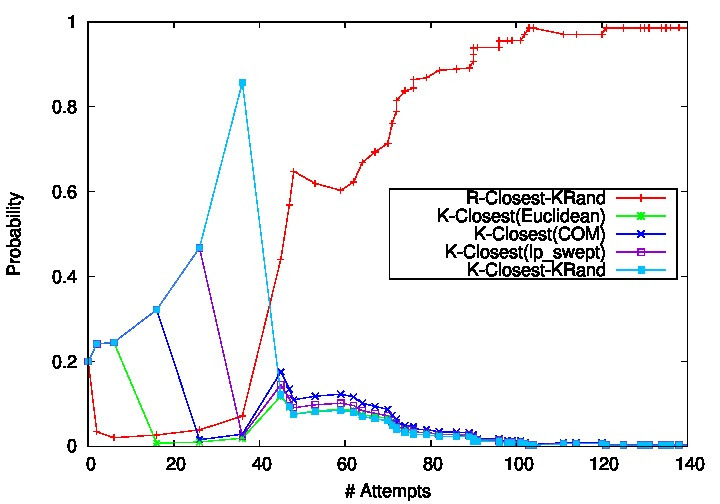
Learning Profile for a U-tunnel Environment |
The maze environment result plots shows the probability that each connection method is selected in the ANC framework over time for a single representative run. Figure 2 shows that early on R-Closest,K-Rand(Euclidean) is selected. However, as roadmap construction progresses, the success of this method begins to level out and the probability of K-Closest,R-Rand(Euclidean) begins to increase and then levels off.
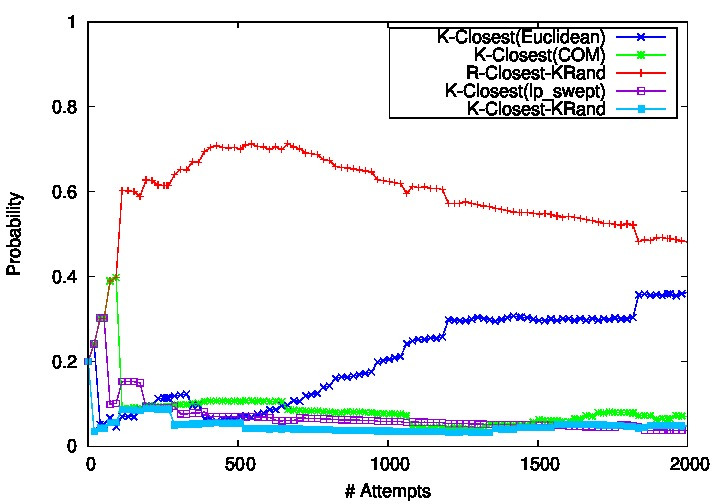
Learning Profile for a maze Environment |
Probabilistic Roadmap Methods (PRMs) solve the motion planing problem by constructing a roadmap (or graph) that models the motion space when feasible local motions exist. PRMs and variants contain several phases during roadmap generation i.e., sampling, connection, and query. Some work has been done to apply machine learning to the connection phase to decide which variant to employ, but it uses a global learning approach that is inefficient in heterogeneous situations.
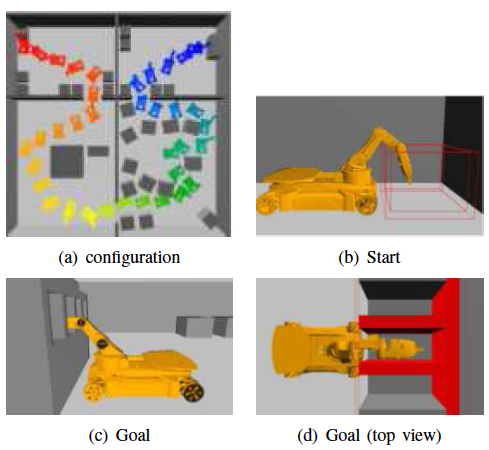
We present an algorithm that instead uses local learning: it only considers the performance history in the vicinity of the current connection attempt and uses this information to select good candidates for connection. It thus removes any need to explicitly partition the environment which is burdensome and typically difficult to do. Our results show that our method learns and adapts in heterogeneous environments, including a KUKA youBot with a fixed and mobile base. It finds solution paths faster for single and multi-query scenarios and builds roadmaps with better coverage and connectivity given a fixed amount of time in a wide variety of input problems. In all cases, our method outperforms the previous adaptive connection method and is comparable or better than the best individual method.
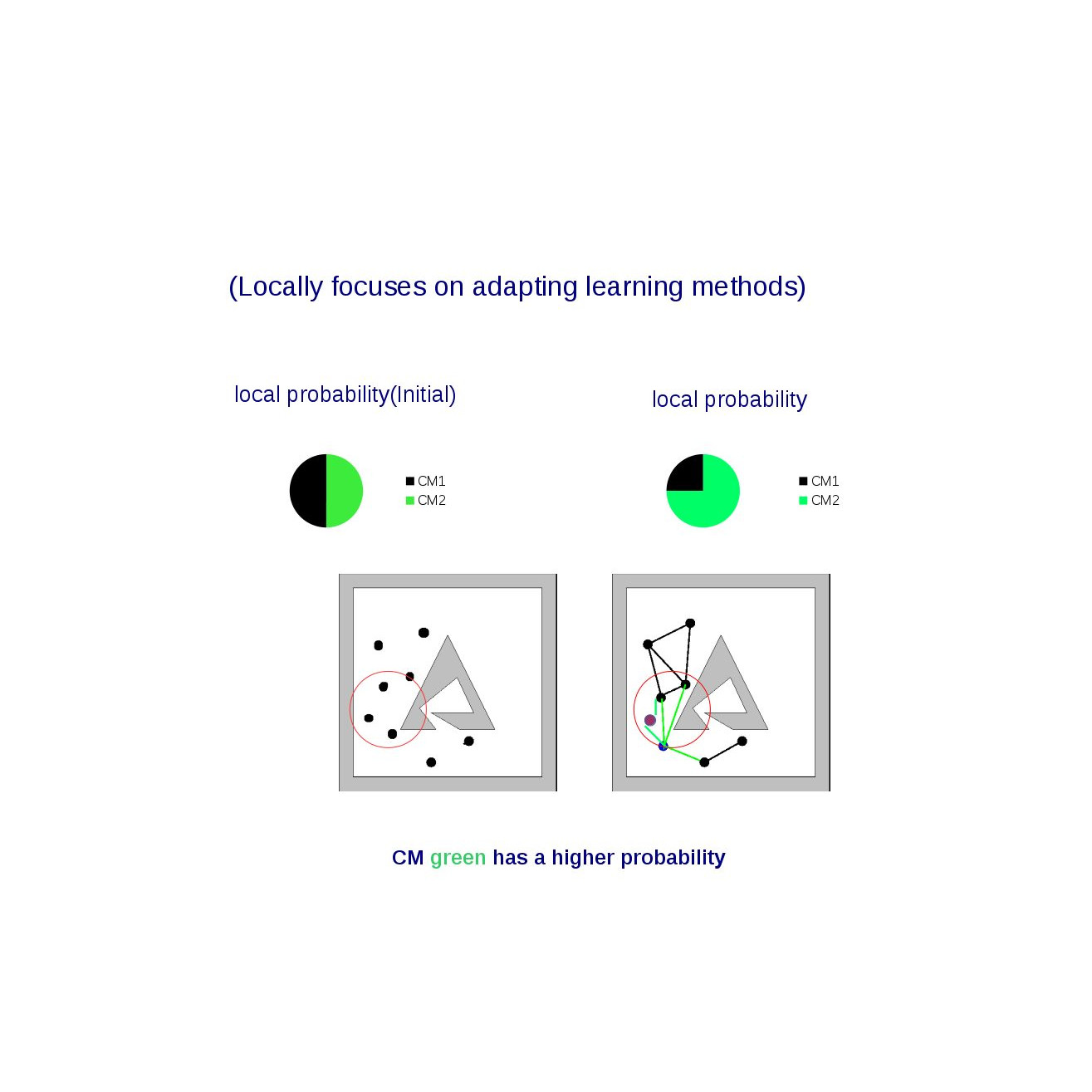
Local learning region |
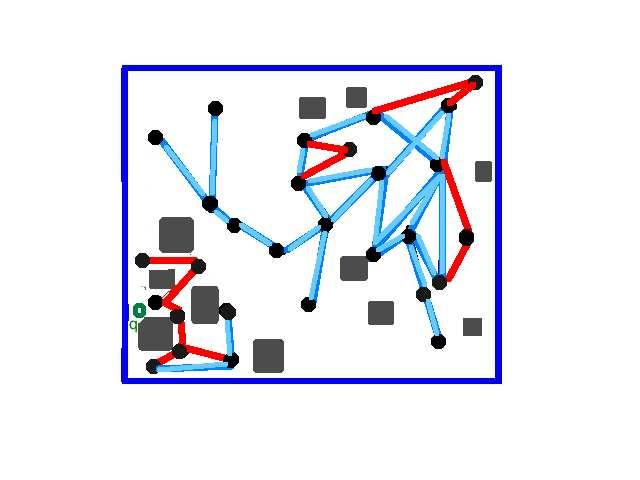
Local learning scenario |
The 36 DOF JellyFish environment consist of a robot has three articulated arms attached to a sphere where each arm has 10 links. The aim of this experiment is to see the performance of ANC-Spatial on a highly articulated and complex robot. Different types of obstacles are placed throughout the envi- ronment. We again provide 8 query samples and count how many possible queries can be solved. Roadmap construction is allowed to take 1500 seconds. Figure 6 (bars in red) shows the percentage of queries (6(a)) and the percentage of nodes in the largest connected components (6(b)) using the StraightLine local planner for each method. ANC-Spatial again solves the greatest percent- age of queries with a higher percentage of its nodes in the largest connected component. ANC-Spatial also outperforms ANC in this articulated linkage environment. This environ- ment is prone to bad partitioning choices because a bad partitioning could easily form a narrow passage that cannot be traversed by this highly articulated linkage. Thus it is even more imperative that localized learning regions are dynamic. Figure 6 (bars in green) shows results using the RotateATS local planner. ANC-Spatial also outperforms the other methods in terms of percentage of queries solved. We also have a good percentage of nodes in the largest connected com- ponent. Even a large change in local planners (as evidenced by changes in individual connection method performance) results in small change in ANC-Spatial performance.
36 DOF JellyFish Environment |
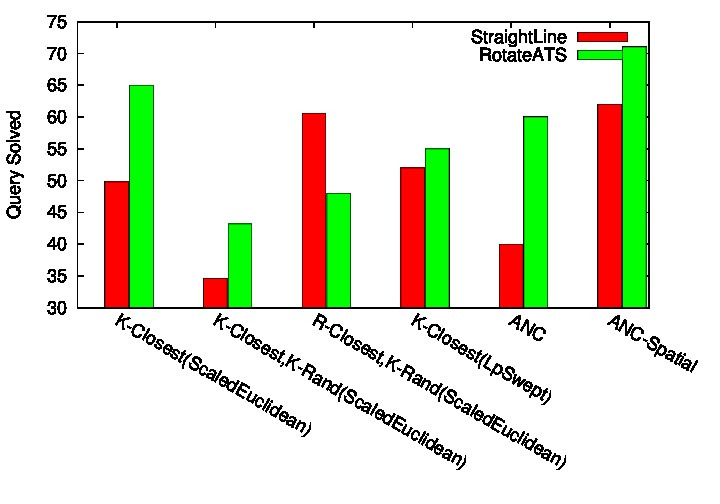
36 DOF JellyFish Time Results |
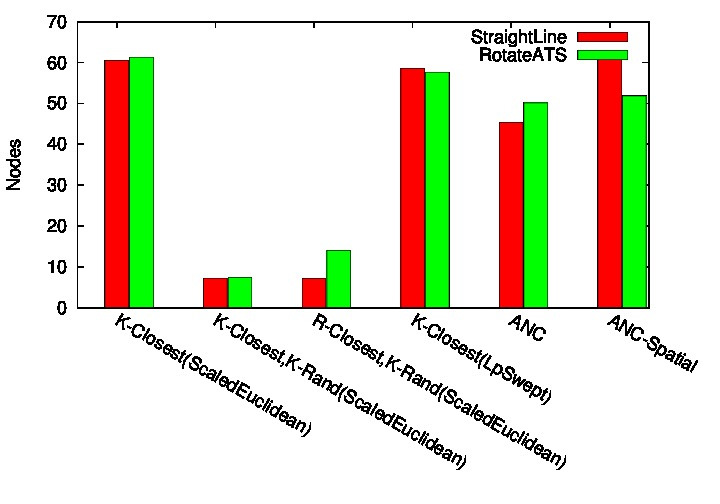
36 DOF JellyFish Node Results> |
|
KukayouBot Environment |
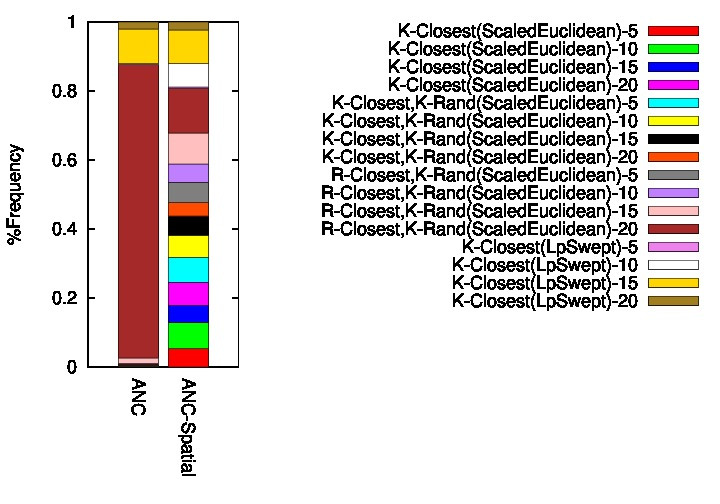
KukayouBot Frequency of Usage |
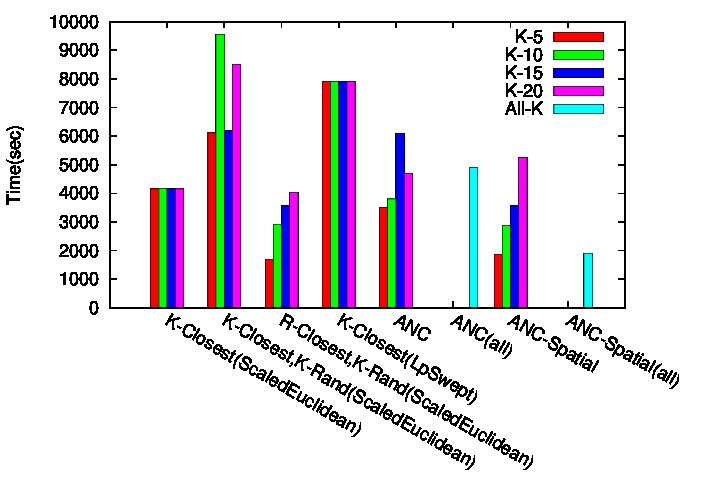
KukayouBot Time Results |
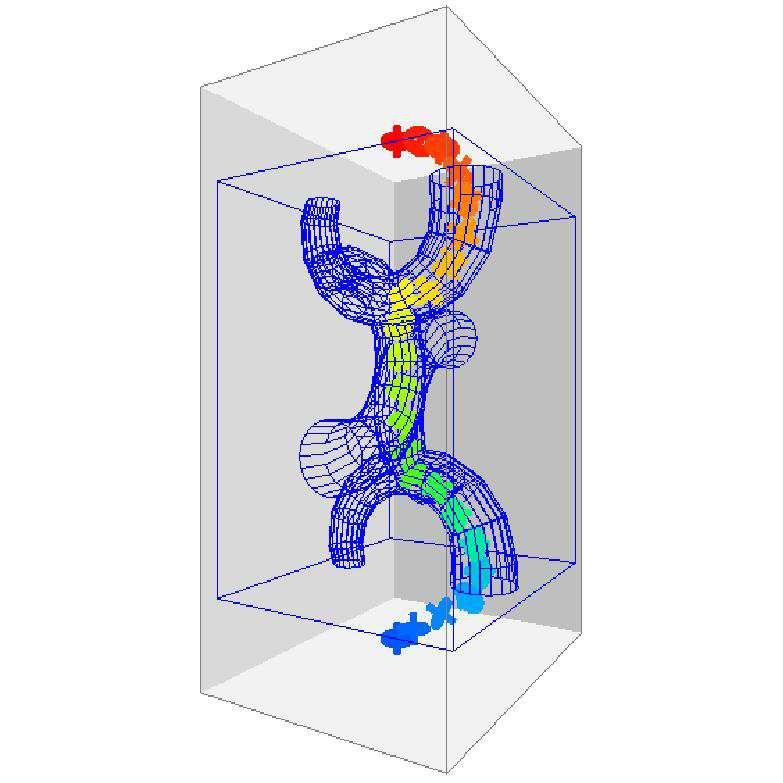
Simulating protein folding motions is an important problem in computational biology. Motion planning algorithms such as Probabilistic Roadmap Methods (PRMs) have been successful in modeling the protein folding landscape. PRMs and variants contain several phases (i.e., sampling, connection, and path extraction). Global machine learning has been applied to the connection phase but is inefficient in situations with varying topology, such as those typical of folding landscapes. Results: We present a local learning algorithm that considers the past performance near the current connection attempt as a basis for learning. It is sensitive not only to different types of landscapes but also to differing regions in the landscape itself, removing the need to explicitly partition the landscape. We perform experiments on 23 proteins of varying secondary structure makeup with 52–114 residues. Our method models the landscape with better quality and comparable time to the best performing individual method and to global learning.
Folding Landscape |
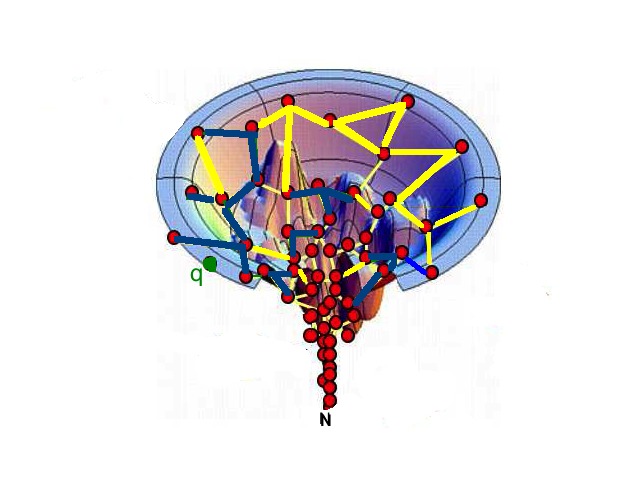
Connection Learning on Folding Landscape |
||
| Applying Learning to Computational Biology | |||
Learning methods outperform the best individual connection methods much of the time: ANC-global produces lower weighted pathways than Cluster, Euclidean, and lRMSD for 11 of the 23 proteins, and ANC-local (blue bars) for 19 of the 23 proteins. Notice, however, that the type of learning is important. ANC-local with its local learning is much more successful than ANC- global with its global approach. In fact, ANC-local is the best approach for 18 out of the 23 proteins studied. ANC-local performs as well as or better than the best performing method for 12 out of 23 proteins (52% of the time), while ANC-global performs best for only 3. Just as with quality, the best performing individual connection method varies between proteins: Euclidean is fastest for 11 proteins, Cluster for 2, and lRMSD for 1. Euclidean is most often the fastest method but is the best method in terms of quality for only 1 protein.
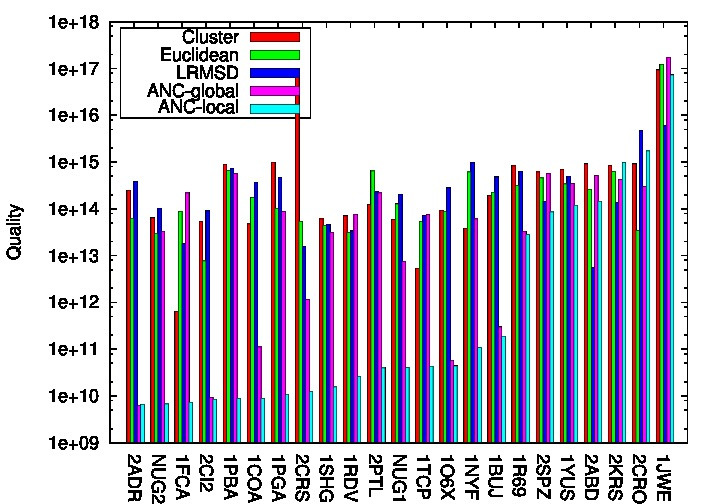
Quality Results |
|||
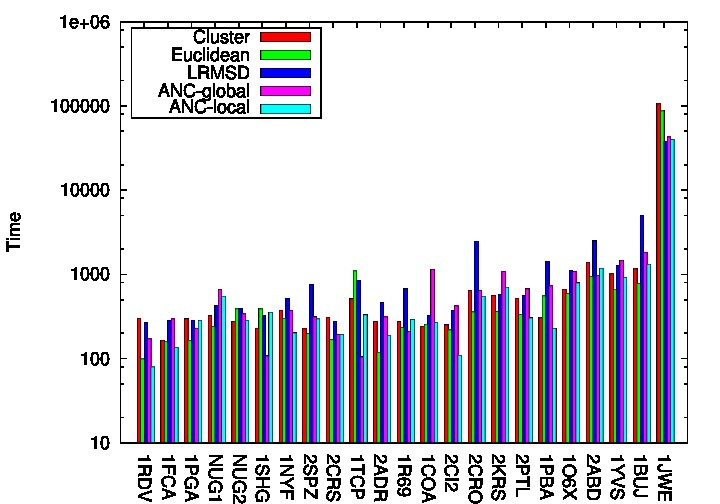
Time Results |
|||
| Applying Learning to Computational Biology | |||