- Improvement in computational efficiency (e.g., collison detection, animation).
- Simplified representations that also improve results for applications such as object matching, object deformation.
Approximate Convex Decomposition (ACD)

Partitioning complex models into ''approximately convex'' regions that allow certain operations to be computed more efficiently.
Skeleton Extraction
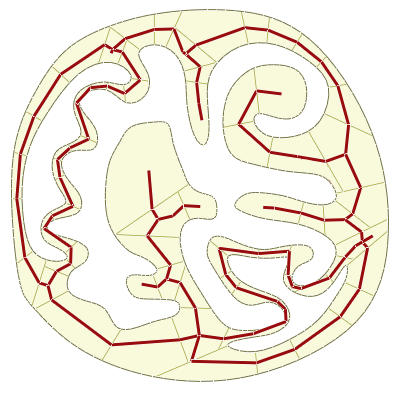
Extracting a simple structure that captures spatial properties of geometric objects
Hierarchical Aggregation
Grouping objects in a geometric scene into approximated ''super-objects'' for faster future processing
Assembly/Disassembly Sequencing

(Dis)assembly sequence planning identifies physically viable plans to (dis)assemble an assembly of parts. It is also used in end-of-life product design to verify the future ability to disassemble the product for recycling or repairs.
Reachability Analysis for Sampling-Based Planning
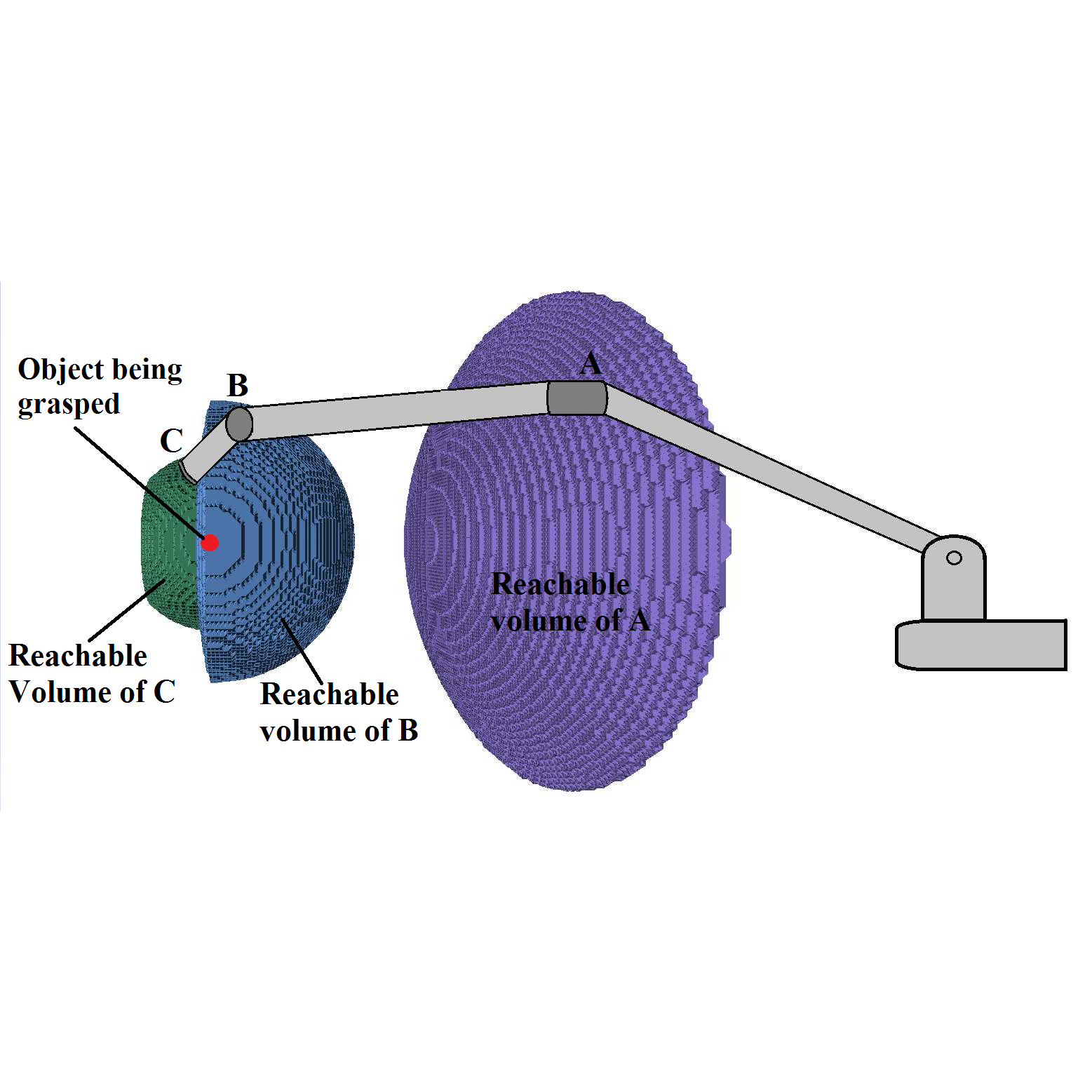
Planning constained motions, such as cooperatively carrying an object, is very hard for sampling-based methods. We have developed specialized methods that exploit reachability analysis for such problems.
Medial Axis Guided Planning
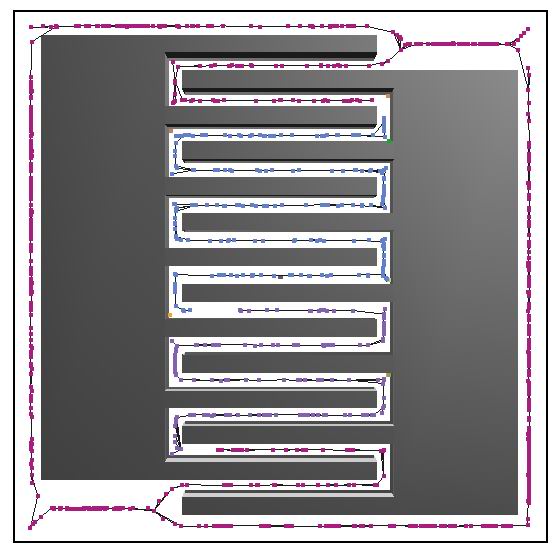
We have developed sampling-based strategies that bias planning towards the medial axis of the planning space, potentially yielding safer paths with higher clearance.
Related Publications
Fast Collision Detection for Motion Planning Using Shape Primitive Skeletons, Mukulika Ghosh and Shawna Thomas and Nancy M. Amato, Algorithmic Foundations of Robotics XIII. Springer Proceedings in Advanced Robotics (SPAR). The 2018 Workshop on the Algorithmic Foundations of Robotics (WAFR), Vol: 14, pp. 36-51, Springer, Cham, May 2020. DOI: 10.1007/978-3-030-44051-0_3 @article{ghosh-wafr-2018 In many robotics applications, the environment (robots and obstacles) often have very complex geometries. These result in expensive primitive computations such as collision detection which in turn, affect the overall performance of these applications. Approximating the geometry is a common approach to optimize computation. Unlike other applications of geometric approximation where it is applied to one space (usually obstacle space), we approximate both obstacle and free workspace with a set of geometric shape primitives that are completely contained within the space and represent its topology (skeleton). We use these âÂÂshape primitive skeletonsâ to improve collision detection performance in motion planning algorithms. Our results show that the use of shape primitive skeletons improves the performance of standard collision detection methods in motion planning problems by 20âÂÂ70% in our 2D and 3D test environments regardless of motion planning strategy. We also show how the same shape primitive skeletons can be used with robots of different sizes to improve the performance of collision detection operation.
Keywords: Collision Detection, Computational Geometry, Motion Planning
Links : [Published] BibTex
, author = "Mukulika Ghosh and Shawna Thomas and Nancy M. Amato"
, title = "Fast Collision Detection for Motion Planning Using Shape Primitive Skeletons"
, journal = "Algorithmic Foundations of Robotics XIII. Springer Proceedings in Advanced Robotics (SPAR)"
, publisher = "Springer, Cham."
, volume = "14"
, pages = "36-51"
, year = "2020"
, doi = "10.1007/978-3-030-44051-0_3"
}
Abstract
Geometric Approximations and Their Application to Motion Planning, Mukulika Ghosh, Doctoral Dissertation, Texas A&M University, College Station, TX, Aug 2019. @phdthesis{ghosh-phd-2019 Geometric approximation methods are a preferred solution to handle complexities (such as a large volume or complex features such as concavities) in geometric objects or environments containing them. Complexities often pose a computational bottleneck for applications such as motion planning. Exact resolution of these complexities might introduce other complexities such as unmanageable number of components. Hence, approximation methods provide a way to handle these complexities in a manageable state by trading off some accuracy. In this dissertation, two novel geometric approximation methods are studied: aggregation hierarchy and shape primitive skeleton. The aggregation hierarchy is a hierarchical clustering of polygonal or polyhedral objects. The shape primitive skeleton provides an approximation of bounded space as a skeleton of shape primitives. These methods are further applied to improve the performance of motion planning applications. We evaluate the methods in environments with 2D and 3D objects. The aggregation hierarchy groups nearby objects into individual objects. The hierarchy is created by varying the distance threshold that determines which objects are nearby. This creates levels of detail of the environment. The hierarchy of the obstacle space is then used to create a decom-position of the complementary space (i.e, free space) into a set of sampling regions to improve the efficiency and accuracy of the sampling operation of the sampling based motion planners. Our results show that the method can improve the efficiency (10 â 70% of planning time) of sampling based motion planning algorithms. The shape primitive skeleton inscribes a set of shape primitives (e.g., sphere, boxes) inside a bounded space such that they represent the skeleton or the connectivity of the space. We apply the shape primitive skeletons of the free space and obstacle space in motion planning problems to improve the collision detection operation. Our results also show the use of shape primitive skeleton in both spaces improves the performance of collision detectors (by 20 â 70% of collision detection time) used in motion planning algorithms. In summary, this dissertation evaluates how geometric approximation methods can be applied to improve the performance of motion planning methods, especially, sampling based motion planning methods
Keywords: Computational Geometry, Convex Decomposition, Sampling-Based Motion Planning
Links : [Published] BibTex
, author = "Mukulika Ghosh"
, title = "Geometric Approximations and Their Application to Motion Planning"
, school = "Department of Computer Science and Engineering, Texas A\&M University"
, month = "August"
, year = "2019"
, note = "https://oaktrust.library.tamu.edu/handle/1969.1/187961"
}
Abstract
Motion Planning using Hierarchical Aggregation of Workspace Obstacles, Mukulika Ghosh, Shawna Thomas, Marco Morales, Sam Rodriguez, and Nancy M. Amato, In Proc. IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), pp. 5716-5721, Daejeon, Korea, Oct 2016. DOI: 10.1109/IROS.2016.7759841 @inproceedings{ghosh2016motion, Sampling-based motion planning is the state-of-the-art technique for solving challenging motion planning problems in a wide variety of domains. While generally successful, their performance suffers from increasing problem complexity. In many cases, the full problem complexity is not needed for the entire solution. We present a hierarchical aggregation framework that groups and models sets of obstacles based on the currently needed level of detail. The hierarchy enables sampling to be performed using the simplest and most conservative representation of the environment possible in that region. Our results show that this scheme improves planner performance irrespective of the underlying sampling method and input problem. In many cases, improvement is significant, with running times often less than 60% of the original planning time.
Keywords: Motion Planning, Workspace Topology
Links : [Published] BibTex
title={Motion planning using hierarchical aggregation of workspace obstacles},
author={Ghosh, Mukulika and Thomas, Shawna and Morales, Marco and Rodriguez, Sam and Amato, Nancy M},
booktitle={2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS)},
pages={5716--5721},
year={2016},
organization={IEEE}
}Abstract
Planning Motions for Shape-Memory Alloy Sheets, Mukulika Ghosh, Daniel Tomkins, Jory Denny, Sam Rodriguez, Marco Morales Aguirre, Nancy M. Amato, Origami, Vol: 6, Issue: 6, pp. 501-511, Dec 2015. DOI: 10.1090/MBK/095.2/13 @inproceedings{Ghosh2015PlanningMF, Shape Memory Alloys (SMAs) are smart materials that can remember predefined shapes. A deformed SMA can transition to a trained shape by applying temperature changes to portions of the material. This reconfigurable property allows SMAs to be used in aeronautics, medicine, and other fields where dynamic re-engineering or actuation of components is required. In this work, we plan the motion of an SMA robot modeled as inflexible regions connected by flexible joints. In this work, we adapt an existing state-of-the-art motion planning algorithm to model the folding of an SMA robot from an unfolded flat state to a folded shape under feasibility constraints such as collision free motion and gravitational stability. Our results validate our model and algorithm by folding interesting 3D shapes using gravitationally stable motions, show flexibility in modeling various planning problems and significantly improved motions in comparable time to not using stability constraints.
Keywords: Computational Geometry, Motion Planning
Links : [Published] BibTex
title={Planning motions for shape-memory alloy sheets},
author={Mukulika Ghosh and D. Tomkins and J. Denny and S. Rodr{\'i}guez and M. Morales and N. Amato},
year={2015}
}Abstract
Fast Approximate Convex Decomposition, Mukulika Ghosh, Texas A&M University, College Station, TX, Aug 2012. TODO: Ghosh, Mukulika (2012). Fast Approximate Convex Decomposition. Master's thesis, Texas A&M University. Available electronically from https : / /hdl .handle .net /1969 .1 /ETD -TAMU -2012 -08 -11873. Approximate convex decomposition (ACD) is a technique that partitions an input object into "approximately convex" components. Decomposition into approximately convex pieces is both more efficient to compute than exact convex decomposition and can also generate a more manageable number of components. It can be used as a basis of divide-and-conquer algorithms for applications such as collision detection, skeleton extraction and mesh generation. In this paper, we propose a new method called Fast Approximate Convex Decomposition (FACD) that improves the quality of the decomposition and reduces the cost of computing it for both 2D and 3D models. In particular, we propose a new strategy for evaluating potential cuts that aims to reduce the relative concavity, rather than absolute concavity. As shown in our results, this leads to more natural and smaller decompositions that include components for small but important features such as toes or fingers while not decomposing larger components, such as the torso that may have concavities due to surface texture. Second, instead of decomposing a component into two pieces at each step, as in the original ACD, we propose a new strategy that uses a dynamic programming approach to select a set of n_c non-crossing (independent) cuts that can be simultaneously applied to decompose the component into n_c + 1 components. This reduces the depth of recursion and, together with a more efficient method for computing the concavity measure, leads to significant gains in efficiency. We provide comparative results for 2D and 3D models illustrating the improvements obtained by FACD over ACD and we compare with the segmentation methods given in the Princeton Shape Benchmark.
Keywords: Computational Geometry, Convex Decomposition
Links : [Published] BibTex
Abstract
Approximate Convex Decomposition of Polyhedra, Jyh-Ming Lien, Nancy M. Amato, Proceedings of the 2007 ACM Symposium on Solid and Physical Modeling (SPM 07), pp. 121-131, Jun 2007. DOI: https://doi.org/10.1145/1236246.1236265 @inproceedings{10.1145/1236246.1236265, Decomposition is a technique commonly used to partition complex models into simpler components. While decomposition into convex components results in pieces that are easy to process, such decompositions can be costly to construct and can result in representations with an unmanageable number of components. In this paper we explore an alternative partitioning strategy that decomposes a given model into "approximately convex" pieces that may provide similar benefits as convex components, while the resulting decomposition is both significantly smaller (typically by orders of magnitude) and can be computed more efficiently. Indeed, for many applications, an approximate convex decomposition (ACD) can more accurately represent the important structural features of the model by providing a mechanism for ignoring less significant features, such as surface texture. We describe a technique for computing ACDs of three-dimensional polyhedral solids and surfaces of arbitrary genus. We provide results illustrating that our approach results in high quality decompositions with very few components and applications showing that comparable or better results can be obtained using ACD decompositions in place of exact convex decompositions (ECD) that are several orders of magnitude larger.
Keywords: Computational Geometry, Convex Decomposition
Links : [Published] BibTex
author = {Lien, Jyh-Ming and Amato, Nancy M.},
title = {Approximate Convex Decomposition of Polyhedra},
year = {2007},
isbn = {9781595936660},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
url = {https://doi.org/10.1145/1236246.1236265},
doi = {10.1145/1236246.1236265},
abstract = {Decomposition is a technique commonly used to partition complex models into simpler components. While decomposition into convex components results in pieces that are easy to process, such decompositions can be costly to construct and can result in representations with an unmanageable number of components. In this paper we explore an alternative partitioning strategy that decomposes a given model into "approximately convex" pieces that may provide similar benefits as convex components, while the resulting decomposition is both significantly smaller (typically by orders of magnitude) and can be computed more efficiently. Indeed, for many applications, an approximate convex decomposition (ACD) can more accurately represent the important structural features of the model by providing a mechanism for ignoring less significant features, such as surface texture. We describe a technique for computing ACDs of three-dimensional polyhedral solids and surfaces of arbitrary genus. We provide results illustrating that our approach results in high quality decompositions with very few components and applications showing that comparable or better results can be obtained using ACD decompositions in place of exact convex decompositions (ECD) that are several orders of magnitude larger.},
booktitle = {Proceedings of the 2007 ACM Symposium on Solid and Physical Modeling},
pages = {121–131},
numpages = {11},
keywords = {concavity measurement, convex decomposition},
location = {Beijing, China},
series = {SPM '07}
}Abstract
Approximate Convex Decomposition and its Applications, Jyh-Ming Lien, Doctoral dissertation, Texas A & M University, College Station, Texas, USA, Dec 2006. DOI: N/A @phdthesis{lien2006approximate, Geometric computations are essential in many real-world problems. One important issue in geometric computations is that the geometric models in these problems can be so large that computations on them have infeasible storage or computation time requirements. Decomposition is a technique commonly used to partition complex models into simpler components. Whereas decomposition into convex components results in pieces that are easy to process, such decompositions can be costly to construct and can result in representations with an unmanageable number of components. In this work, we have developed an approximate technique, called Approximate Convex Decomposition (ACD), which decomposes a given polygon or polyhedron into "approximately convex" pieces that may provide similar benefits as convex components, while the resulting decomposition is both significantly smaller (typically by orders of magnitude) and can be computed more efficently. Indeed, for many applications, an ACD can represent the important structural features of the model more accurately by providing a mechanism for ignoring less significant features, such as wrinkles and surface texture. Our study of a wide range of applications shows that in addition to providing computational efficiency, ACD also provides natural multi-resolution or hierarchical representations. In this dissertation, we provide some examples of ACD's many potential applications, such as particle simulation, mesh generation, motion planning, and skeleton extraction.
Keywords: Computational Geometry, Convex Decomposition
Links : [Published] BibTex
title={Approximate convex decomposition and its applications},
author={Lien, Jyh-Ming},
volume={69},
number={01},
year={2006}
}Abstract
Approximate Convex Decomposition, Jyh-Ming Lien, Nancy M. Amato, Proceedings of the Twentieth Annual Symposium on Computational Geometry (SOCG 04), pp. 457-458, Brooklyn, New York, Jun 2004. DOI: 10.1145/997817.997889 @inproceedings{ la-acd-04 Not applicable (it is a video abstract)
Keywords: Computational Geometry
Links : [Published] BibTex
, author = "J.-M. Lien and N. M. Amato"
, title = "Approximate Convex Decomposition"
, booktitle = "Proc.\ 20th Annual {ACM} Symp.\ Computat.\ Geom.\ (SoCG)"
, year = "2004"
, month = "June"
, note = "Video Abstract."
, pages = "457--458"
}
Abstract
Approximate Decomposition of Polygons, Jyh-Ming Lien, Nancy M. Amato, Proceedings of the Twentieth Annual Symposium on Computational Geometry (SOCG 04), pp. 17-26, Brooklyn, New York, Jun 2004. DOI: 10.1145/997817.997823 @inproceedings{ la-acdp-04 We propose a strategy to decompose a polygon, containing zero or more holes, into ``approximately convex'' pieces. For many applications, the approximately convex components of this decomposition provide similar benefits as convex components, while the resulting decomposition is significantly smaller and can be computed more efficiently. Moreover, our approximate convex decomposition (ACD) provides a mechanism to focus on key structural features and ignore less significant artifacts such as wrinkles and surface texture a user specified tolerance determines allowable concavity. We propose a simple algorithm that computes an ACD of a polygon by iteratively removing (resolving) the most significant non-convex feature (notch). As a by product, it produces an elegant hierarchical representation that provides a series of `increasingly convex' decompositions. Our algorithm computes an ACD of a simple polygon with n vertices and r notches in O(nr) time. In contrast, exact convex decomposition is NP-hard or,if the polygon has no holes, takes O(nr2) time.
Keywords: Computational Geometry, Convex Decomposition
Links : [Published] BibTex
, author = "J.-M. Lien and N. M. Amato"
, title = "Approximate Convex Decomposition of Polygons"
, booktitle = "Proc.\ 20th Annual {ACM} Symp.\ Computat.\ Geom.\ (SoCG)"
, year = "2004"
, month="June"
, pages = "17--26"
}
Abstract
A Probabilistic Method for Rigid-Body Motion Planning Using Sampling from the Medial Axis of the Free Space, Steven A. Wilmarth, Doctoral Dissertation, Texas A&M University, pp. 1-108, Dec 1999. @phdthesis{wilmarth-phd-1999 Motion planning in the presence of obstacles is an important problem in robotics with numerous applications in other areas. While complete motion planning algorithms do exist, they are rarely used in practice since they are computationally infeasible in all but the simplest cases. For this reason, many recent efforts have focused on probabilistic methods, which sacrifice completeness in favor of computational feasibility and applicability. In particular, several algorithms, known as probabilistic roadmap planners, have been shown to perform well in a number of practical situations; however, their performance degrades when paths are required to pass through narrow passages in the free space. In this dissertation we present a method of sampling the configuration space of a rigid body moving in three dimensions in which randomly generated configurations are retracted onto the medial axis of the free space. We develop some theory of the medial axis on the configuration space SE(3) and present algorithms that perform the retraction while avoiding explicit computation of the medial axis. Finally, we give some preliminary experimental results demonstrating the performance of the algorithm.
Keywords: Computational Geometry, Medial Axis, Sampling-Based Motion Planning
Links : [Published] BibTex
, author = "Steven A. Wilmarth"
, title = "A Probabilistic Method for Rigid-Body Motion Planning Using Sampling from the Medial Axis of the Free Space"
, school = "Department of Mathematics, Texas A\&M University"
, year = "1999"
, month = "December"
}
Abstract
Motion planning for a rigid body using random networks on the medial axis of the free space, Steven A. Wilmarth, Nancy M. Amato, Peter F. Stiller, Proceedings of the Annual Symposium on Computational Geometry (SOCG), pp. 173-180, Jun 1999. DOI: 10.1145/304893.304967 @INPROCEEDINGS{was-mprb-99, Several motion planning methods using networks of randomly generated nodes in the free space have been shown
to perform well in a number of cases, however their performance
degrades when paths are required to pass through narrow
passages in the,jree space. In [16] we proposed MAPRM,
a method of sampling the configuration space in which randomly
generated configurations, free or not, are retracted
onto the medial axis of the free space without having to first
compute the medial axis; this was shown to increase sampling
in narrow passages. In this paper we give details of
the MAPRM algorithm for the case of a free-flying rigid
body moving in three dimensions, and show that the retraction
may be carried out without explicitly computing the C-obstacles
or the medial axis. We give theoretical arguments
to show that this improves sampling in narrow corridors, and
present preliminary experimental results comparing the performance
to uniform random sampling from the free space.
Keywords: Computational Geometry, Medial Axis, Sampling-Based Motion Planning
Links : [Published] BibTex
author={Steven A. Wilmarth and and Nancy M. Amato and Peter F. Stiller},
booktitle={Proceedings of the Annual Symposium on Computational Geometry}
title={Motion Planning for a Rigid Body Using Random Networks on the Medial Axis of the Free Space},
year={1999},
pages={173-180},
doi={10.1145/304893.304967}}Abstract
Parallel Algorithms for Convex Hulls and Proximity Problems, Nancy M. Amato, University of Illinois Urbana-Champaign, Jan 1995. @phdthesis{amato-phd-1995 Computational geometry is concerned with the algorithmic aspects of solving geometric problems. The problems are motivated from and have application to such diverse areas as computer graphics, robotics, computer vision, and operations research. Problems arising from these areas of application are good candidates for parallelization since they often have both intense computational needs and stringent response time requirements. Motivated by these concerns, this thesis investigates parallel algorithms for some basic geometric problems. The model of parallel computation used in our studies is the Parallel Random Access Machine (CREW PRAM).
Keywords: Computational Geometry, High-Performance Computing, Parallel Algorithms
Links : [Published] BibTex
, author = "Nancy M. Amato"
, title = "Parallel Algorithms for Convex Hulls and Proximity Problems"
, school = "Department of Computer Science, University of Illinois at Urbana-Champaign"
, year = "1995"
, month = "January"
, note = "https://search.proquest.com/openview/a46d67f1f648ab5badf409ac3ed51894/1?pq-origsite=gscholar&cbl=18750&diss=y"
}
Abstract
