Task Allocation

TMP-CBS

This work presents a multi-robot integrated task and motion planning method capable of finding solutions for multiply decomposable tasks with sequential subtask dependencies which are optimal w.r.t. the state space representation.

We focus on transportation-like tasks where the objectives of a task correspond to physical locations in the environment. In the simplest example, a transportation task is defined by the movement of an object between a pick-up and a delivery location. We present an approach that finds a solution to a set of transportation tasks for a heterogeneous multi-robot system (MRS) with varying capabilities while leveraging inter-robot interactions. These interactions allow the task object to be handed from one robot to another.

The option to interact in this way creates multiply decomposable tasks. Optimal multi-robot solutions for multiply decomposable tasks require coupled computation of the task decomposition, subtask allocation, and robot motion plans.

Traditional integrated task and motion planning (TMP) methods are designed for single-robot systems and do not naturally contain multi-robot semantics. They do not easily account for multi-robot collisions during motion planning and would need to treat the entire MRS as a single composite agent to address this, which quickly becomes intractable as the size of the robot team increases.

Previous multi-robot work handles parts of this with varying coupled and decoupled natures. To the best of our knowledge, our approach is the first to couple all three parts to find the best available solution for these multiply decomposable tasks.

Algorithm

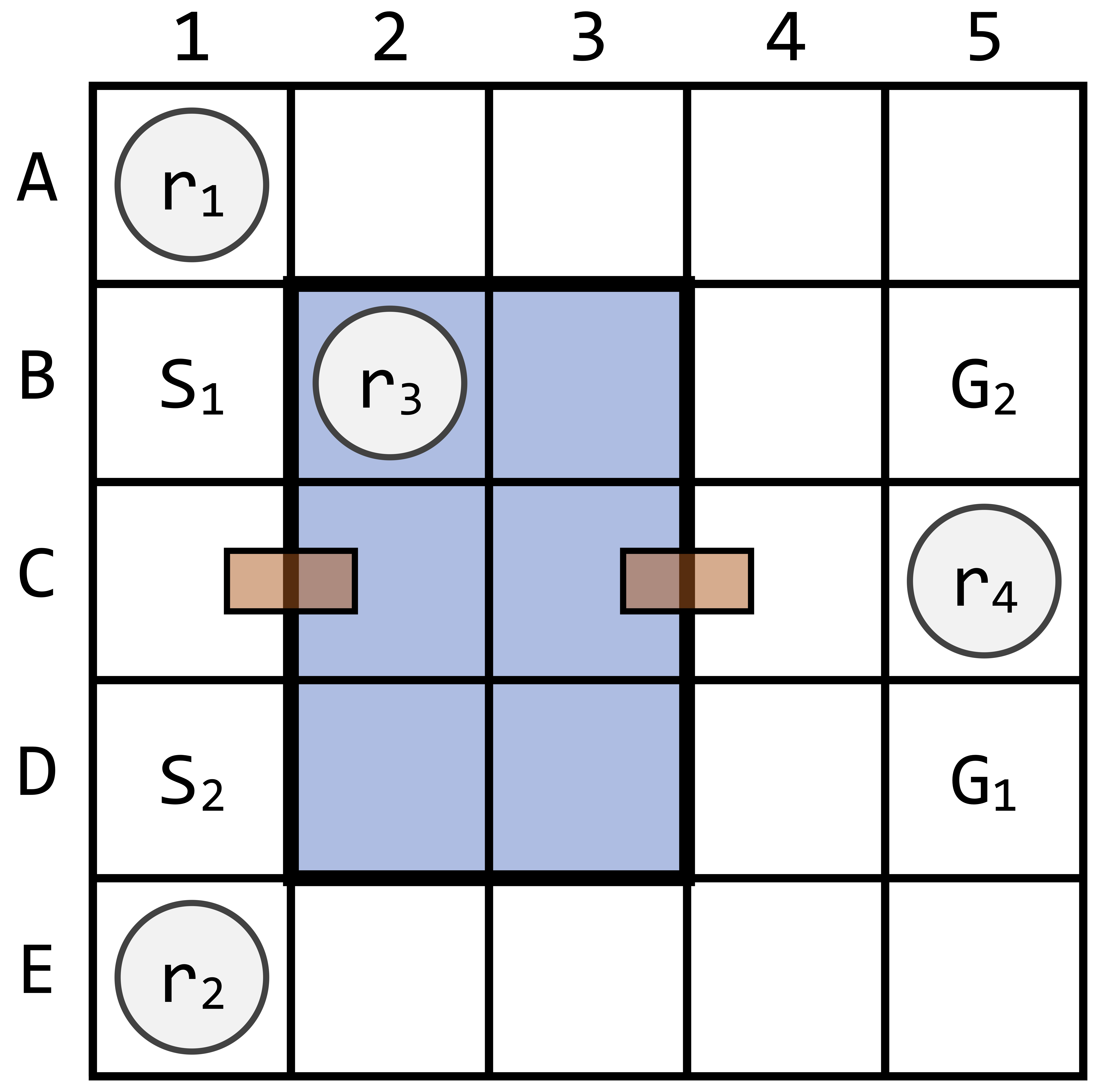
We present integrated Task and Motion Planning Conflict-Based Search (TMP-CBS) as the first multi-robot task and motion planner for multiply decomposable tasks with sequentially dependent subtasks which can extract team plans that are optimal with respect to the current individual robot roadmaps. We first outline the Conflict-Based Search (CBS) algorithm by Sharon et. al.. We then map the CBS approach to task planning. Finally, we integrate the task planner with CBS and CBS-MP~\cite{ssma-romrmpucbs-19}. The task component is the same for both discrete and continuous problems, so our explanation and example (the grid image on the left) will use CBS and a discrete grid roadmap for clarity of exposition.

CBS

CBS is a multi-robot pathfinding (MRPF) algorithm that finds the optimal set of conflict free paths for a set of robots. It first plans for all robot paths individually, and then iteratively finds and resolves conflicts between these paths where a conflict is defined by two robots occupying the same vertex or edge in the roadmap at the same time. The method uses a low-level pathfinding method to find individual robot paths and a high-level Conflict Tree (CT) in order to manage conflicts.

Nodes in the CT contain a solution to the MRPF problem consisting of the set of individual robot paths, a solution cost, and a set of path constraints for each robot. The root node is the initial path found for all robots with no constraints. The method selects the cheapest unprocessed node in the tree and checks for conflicts between paths. If no conflicts are found, the goal node is returned containing the optimal solution.

When a conflict is discovered within a CT node, the conflict is resolved by splitting the node into two children, one for each robot. Both children inherit the set of path constraints for each robot from the parent node. Each child is given an additional constraint for one of the conflicting robots at the time and location of the conflict, and the path for that robot is replanned with the new constraint. Thus a node exists for both possibilities where either robot is given precedence for that location at that time. CBS guarantees optimality by examining both possibilities as a node is split into two children for all conflicts.

Task Planning

In this work, we propose to adapt the CBS algorithm to the problem of solving a set of tasks given a set of robots. A node in the adapted CT contains a solution and a set of constraints. The solution consists of a decomposition, allocation, and corresponding subtask paths for each individual task. The constraint set is comprised of two subsets, motion constraints and allocation constraints. A motion constraint is the same as in CBS (robot r, vertex v, time x) with an additional task component indicating that the motion constraint only affects the robot r when it is planning for a subtask si in task t for a constraint notion of (t,r,v,x).

An allocation constraint indicates a time interval with a start/end location between which a robot is unavailable for the constrained task. A task plan satisfying an allocation constraint ensures that the robot is able to reach the start location of the constraint at the beginning of the constraint time interval and does not require the robot to arrive at any location at a time earlier than the robot can reach following the end of the allocation constraint. Allocation constraints usually correspond to other subtasks assigned to the robot in question and the time intervals and start/end locations associated with those subtasks. We denote an allocation constraint (t,r,s) with task t, robot r, and subtask allocation s containing the time interval and start/end locations.

Low-Level Search In the initial pathfinding CBS algorithm, the goal is to find a set of feasible collision-free robot paths. These individual paths are computed with a low-level pathfinding algorithm. The authors use A* over a two dimension location x time search space in the original work for this. We map this concept to task space by creating a unified representation for task, motion, and robot availability semantics so that searching over it produces the optimal task decomposition, allocation, and robot motions.

In our previous work on Interaction Templates, we developed a combined roadmap that integrates task semantics within a set of roadmaps for all robot-types in the system. This is used to capture inter-robot interactions exchanging the payload in transportation tasks. Virtual nodes are used to represent the initial pick-up and delivery locations with 0 weight edges connecting the virtual nodes to valid robot configurations at those locations. Plans across the combined roadmap produce task decompositions and preliminary motion plans for the individual subtasks. The costs associated with the subtasks in the decomposition assume that a robot is immediately available to perform each subtask and thus does not account for time taken for robots to travel to the subtask start location. Additionally, it relies upon reactive collision avoidance behavior and does not include the cost of collision avoidance in the cost of subtasks when computing the decomposition either. Here we expand the combined roadmap representation to capture robot availability and use the CBS structure to account for motion collisions.

The CBS conflict tree approach results in repeated searching of the space, so we construct the task graph, a condensed representation of the combined roadmap. Vertices in the task graph correspond to subtask start/end locations which in our combined roadmap correspond to interaction locations where robots can exchange a payload and the virtual nodes for the task's initial pick-up and final delivery locations. Edges between these vertices correspond to paths in the combined roadmap between these locations.

For example, in the lake scenario depicted in the left figure the docks located at (C1,C2) and (C3,C4), are interaction locations and thus correspond to possible subtask start/end vertices in the task graph (the two land-water vertex pairs in Task Graph depicted in the middle figure). The task graph, corresponds to task t1 defined by pick-up/delivery locations S1,G1 in Fthe example environment on the left. S1 in the task graph is the virtual start node, and SL is the land robot subtask start at B1. The edge between SL and the left land vertex corresponds to the path (B1,C1) in the example environment.

A plan across the task graph produces a decomposition for a task without considering robot availability. This produces solutions similar to the IT method which assumes robot availability. This can lead to suboptimal decompositions as it does not account for the time taken for a robot to reach a subtask start or for allocations of a robot to subtasks outside of the current task.

For example, when considering the example environment, both tasks would compute a decomposition of three subtasks (land, water, land) with an interaction between each subtask. The middle water subtask for both tasks must be assigned to r3, thus forcing one of the task plans to have an extended first land subtask, as r1 or r2 waits on r3 to return to perform its second subtask. While this is a valid solution, it is suboptimal as the decomposition could instead consist of a single subtask directly transporting the payload from the pick-up to the delivery location arriving earlier than waiting for r3 to become available again.

To address this, we add another dimension to our representation denoting robot availability. As considering every time step each robot is available will lead to a drastic increase in the search space, we condense contiguous intervals of robot availability for each vertex in the task graph. This represents the first instance a robot is able to start a subtask% at the location corresponding to the task graph vertex and the last instance the robot is able to complete a subtask at the location corresponding to the task graph vertex before violating an allocation constraint (usually this indicates leaving for another allocation). A search over this space produces an optimal individual task plan (decomposition and allocation) w.r.t. the existing allocation constraints of the robots.

This is modeled after the Safe Interval Path Planning technique by Phillips et. al., which condenses the time dimension of a search space with constraints from dynamic obstacles or other robots. In the availability interval graph depicted on the right, the expansion of the land start node SL by robot availability and the connections to the virtual start node are shown. S_r4 has an availability interval of 7 to infinity as robot r4 can reach the start location at time 7.

The high-level search (show in the pseudocode) builds a CT tree to iteratively build an optimal plan for a set of transportation tasks and a set a robots. CT nodes contain a solution for the set of tasks consisting of decompositions, allocations, and corresponding motion plans.

We build upon CBS conflict detection and resolution, by adding an allocation conflict. An allocation conflict between two tasks t1, t2 is defined by the allocation of the same robot r to a subtask in both tasks si in t1, sj in t2 such that assignment time of r to si and sj is overlapping, or the minimum time r can reach the start location of sj after completing si is greater than the assigned time of r to sj.

Upon detection of an allocation conflict C=(t1, t2, r, si, sj), two child nodes are created, one for each task involved in the conflict. Both child nodes receive the parent node's solution and constraint set, and each child node is given one additional allocation constraint for its corresponding task, (t1, r, sj) and (t2, r, si) as shown on line 17 in the psuedocode. A new low-level plan is then computed for the corresponding task in each node that extit{recomputes} the decomposition, allocation, and motion plan by searching the unified representation. This allows limitations on robot availability to affect the task decomposition.

This process can be seen in the conflict tree for the example lake scenario. Both initial individual task plans use r3 during overlapping intervals creating an allocation conflict. This is resolved by creating a child node for each task with a new constraint corresponding to the other task's allocation of r3. The updated solution for each child is shown in the conflict tree.

Integration of Task and Motion Planning

If we only considered allocation conflicts when evaluating a CT node, we will produce solutions similar to other allocation and pathfinding methods where the separation of task allocation and collision-free path planning leads to inconsistencies in the costs used for allocation and the costs of the collision-free paths (the distinction still standing that we additionally simultaneously compute the decomposition for a complete task planning approach instead of just task allocation). The cost of a robot executing a subtask in the task graph is dependent upon the path it takes between subtask start/end locations as well as the time spent waiting on the next robot to reach the exchange the point. When motion conflicts are considered the cost of this path can be altered by a longer path being required either for the transition of a robot from the end of one subtask to the start of another or the path taken during execution of the subtask.

Instead, we want an integrated TMP method to account for possible motion conflicts. As mentioned previously, the task components are the same for both discrete CBS and continuous CBS-MP. We will explain the integration w.r.t. to CBS for clarity of the exposition and examples. A motion conflict M=(ti,ri,tj,rj,v,x) is defined by a pair of robots ri, rj, the tasks they are currently executing a subtask of ti, tj, the vertex v the robots occupy in the plan, and a time x at which the robots occupy v in the plan (motion conflicts can also occur along edges, but we point the reader to the CBS and CBS-MP works for details as we handle them in the same fashion).

The method first checks for allocation conflicts, and if none are found checks for motion conflicts. The edges in the unified task graph-availability space correspond to paths between subtask start/end locations in the underlying combined roadmap. To check for motion conflicts, the paths of the current task plans are extracted and validated.

The complete path for each robot across all of its allocations is compiled. These paths now mirror the paths checked for conflicts in CBS or CBS-MP, and conflicts are found in the same manner. The only distinction is tracking which task each robot is currently allocated to throughout robot paths.

Upon discovering a conflict, two child nodes are created, one for each task-robot (ti,ri), (tj,rj) pair. Both child nodes are given the solution and constraint set of the parent, and each is given an additional motion constraint for the task-robot pair, Mi=(ti,ri,v,x)and Mj=(tj,rj,v,x) respectively. Given the new motion constraint, the transition costs for the robot in the unified task graph-availability space are updated in the respective node. The low-level search is invoked to update the individual task plan (decomposition, allocation, and corresponding motion plans). This allows collision avoidance to affect the decomposition and allocation. The method continues to evaluate the next best node in the CT tree until the first conflict-free node is discovered. This node contains the optimal solution complete with the decomposition, allocation, and motion plans.% for the set of tasks.}

Considering these motion constraints results in changes to the available intervals as well as the cost of traversing edges in the task search space. As the cost of a path between two locations depends upon the start time of that path, the cost of traversing an edge in the unified representation space must be computed by a search in the underlying roadmap w.r.t. the motion constraints for that robot during search time. These costs are then validated with the availability intervals to find optimal paths in task space w.r.t. both the task allocation constraints and the motion constraints. The two-level search framework discovers and resolves both types of conflicts to produce the optimal multi-robot task plan.

When considering the first lower node in the CT for the lake scenario (depicted in the horizontal tree image), although there are no task conflicts, there is a path conflict at timestep 6 with R4 and R2 both being at D4 while performing T1 and T2 respectively. The path conflict is converted to constraints and the node branched the same as CBS/CBS-MP with the addition of the constraint being unique to the individual task being planned.

Related Publications

Multi-Robot Task and Motion Planning with Subtask Dependencies, James Motes, Read Sandstrom, Hannah Lee, Shawna Thomas, Nancy M. Amato, IEEE Robotics and Automation Letters (RA-L), Vol: 5, Issue: 2, pp. 3338-3345, Feb 2020. DOI: 10.1109/LRA.2020.2976329
Keywords: Motion Planning, Multi-Agent, Task Planning
Links : [Published]

BibTex

@article{motes2020multi,
title={Multi-Robot Task and Motion Planning With Subtask Dependencies},
author={Motes, James and Sandstr{\"o}m, Read and Lee, Hannah and Thomas, Shawna and Amato, Nancy M},
journal={IEEE Robotics and Automation Letters},
volume={5},
number={2},
pages={3338--3345},
year={2020},
publisher={IEEE}
}

Abstract

We present a multi-robot integrated task and motion method capable of handling sequential subtask dependencies within multiply decomposable tasks. We map the multi-robot pathfinding method, Conflict Based Search, to task planning and integrate this with motion planning to create TMP-CBS. TMP-CBS couples task decomposition, allocation, and planning to support cases where the optimal solution depends on robot availability and inter-team conflict avoidance. We show improved planning time for simpler task sets and generate optimal solutions w.r.t. the state space representation for a broader range of problems than prior methods.