Project Alumni: Troy McMahon, Xinyu Tang, Li Han
Supported By: NSF, Texas Higher Education Coordinating Board
 |
Sometimes motion planning problems include constraints such as the grippers must maintain contact with an object being manipulated (closure constraints) or that parts of the robot must (or cannot) occupy certain subsets of the workspace. Such problems are particularly challenging for sampling-based methods since it is difficult to generate samples that satisfy these constraints. In a series of results, we have developed specialized sampling-based planning methods that can efficiently generate samples that satisfy such constraints.
We introduce a new concept, called reachable volumes, that are a geometric representation of the regions the joints and end effectors of a robot can reach, and use it to define a new planning space called RV-space where all points automatically satisfy robot-specific constraints. Constraints include joint closure constraints and constraints on the position of individual joints (including the end effector).
Samples and paths generated in RV-space naturally conform to constraints, making planning for constrained systems no more difficult than planning for unconstrained systems. Consequently, constrained motion planning problmes that were previously difficult or unsolvable become manageable and in many cases trivial.
This method is applicable to high dof linkages, closed chains and tree-like robots with spherical, prismatic and planar articulated joints (and combinations thereof). Reachable volumes can be used to guide robot design and assist in robot operation by allowing the operator to see what portions of the robot can reach.
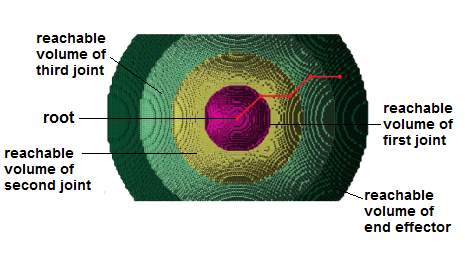
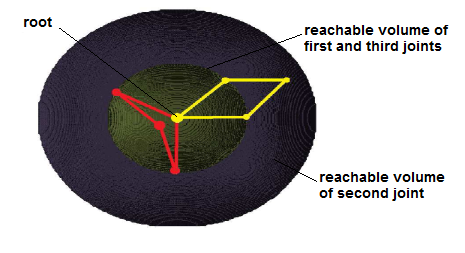
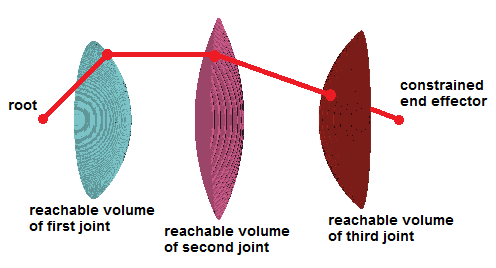
Reachable Volumes Illustrations
Reachable Volumes can handle both unconstrained and constrained systems that include a variety of joint types. In this video we define reachable volumes and show how they are computed. We also show visualizations of the reachable volumes for a number of example robots.
RV-space encodes the intrinsic constraints of the robot. It is independent of the environment. Just as with traditional configuration space (C-space), collision checking must be preformed separately. Below, we provide visualizations of the reachable volumes for several different linkages. In each example, the linkage is displayed in red, and the reachable volume for each joint is shaded in a different color.
Reachable Volume Sampling
We also develop a family of samplers that use reachable volumes to generate samples for a wide variety of motion planning problems including end effector constraints, closure constraints, and constraints on joint positions with as many as 256 dof. The following video summarizes how reachable volume sampling works for different example environments:
Reachable Volume sampling iteratively places joints in their available reachable volume until all joints have been placed. Before any joints are placed, all joints have their orignial/full reachable volume. Once a joint is placed, this implies an additional constraint to the system which restricts the available reachable volume of other joints (e.g., neighboring joints). To place a joint, we first compute its updated reachable volume based on any previously placed joints. We then randomly select a joint placement from this reduced set.
For example, consider the following 6 link fixed-base grasper with constraints placed on the 2 end effectors (red and green regions in the top left image).
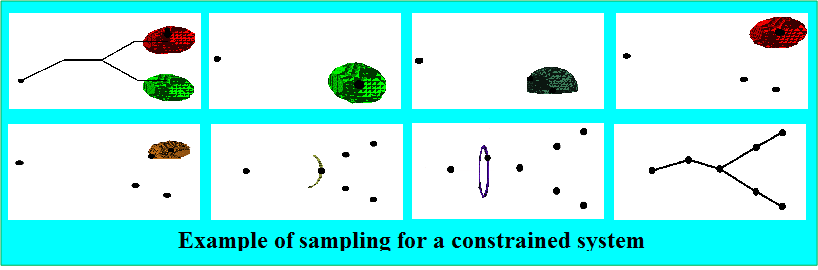
Sampling proceeds as follows (right to left, top to bottom in image):
At each placement, the unplaced reachable volumes become restricted.
Reachable Volume Local Planning
We also present a reachable volume-based local planner. Just like the sampler, it guarantees that the local plan will satisfy constraints. The local planner works by interatively stepping joints in RV-space and updating affected available reachable volumes:
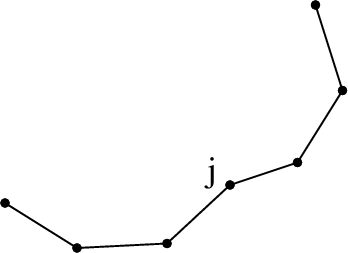
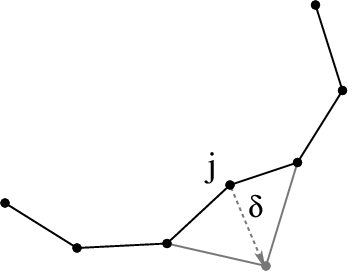
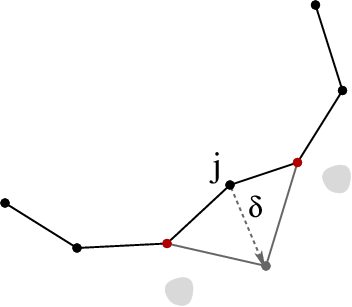
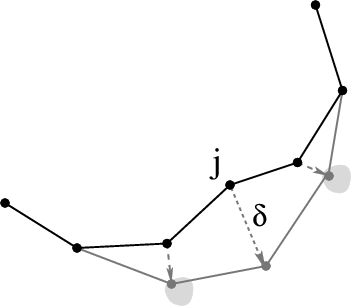
Reachable Volume Distance Metric
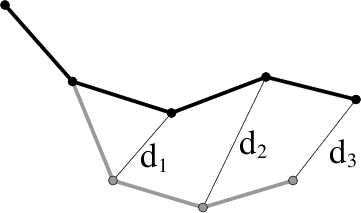
The reachable volume distance metric captures the distance traversed during reachable volume stepping (and local planning). It is a weighted sum of the Euclidean distance between the robot base placements in workspace and the Euclidean distance between the joints placements in RV-space.
Reachable Volume Performance in Practice
We consider a variety of environments and study robots with 19 to 262 dof:

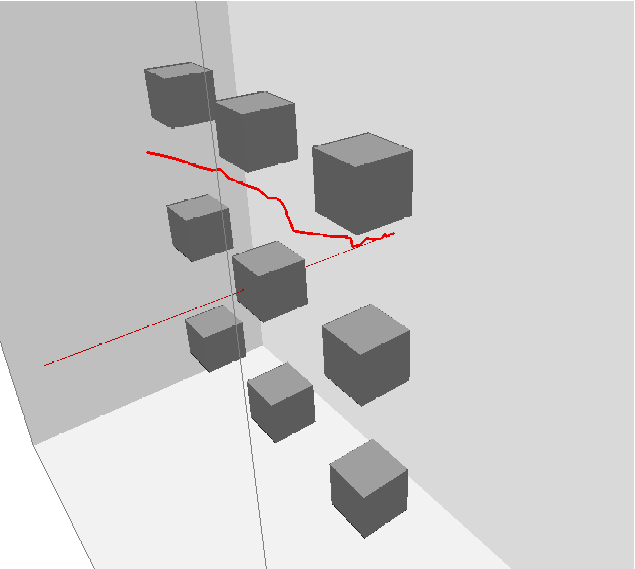
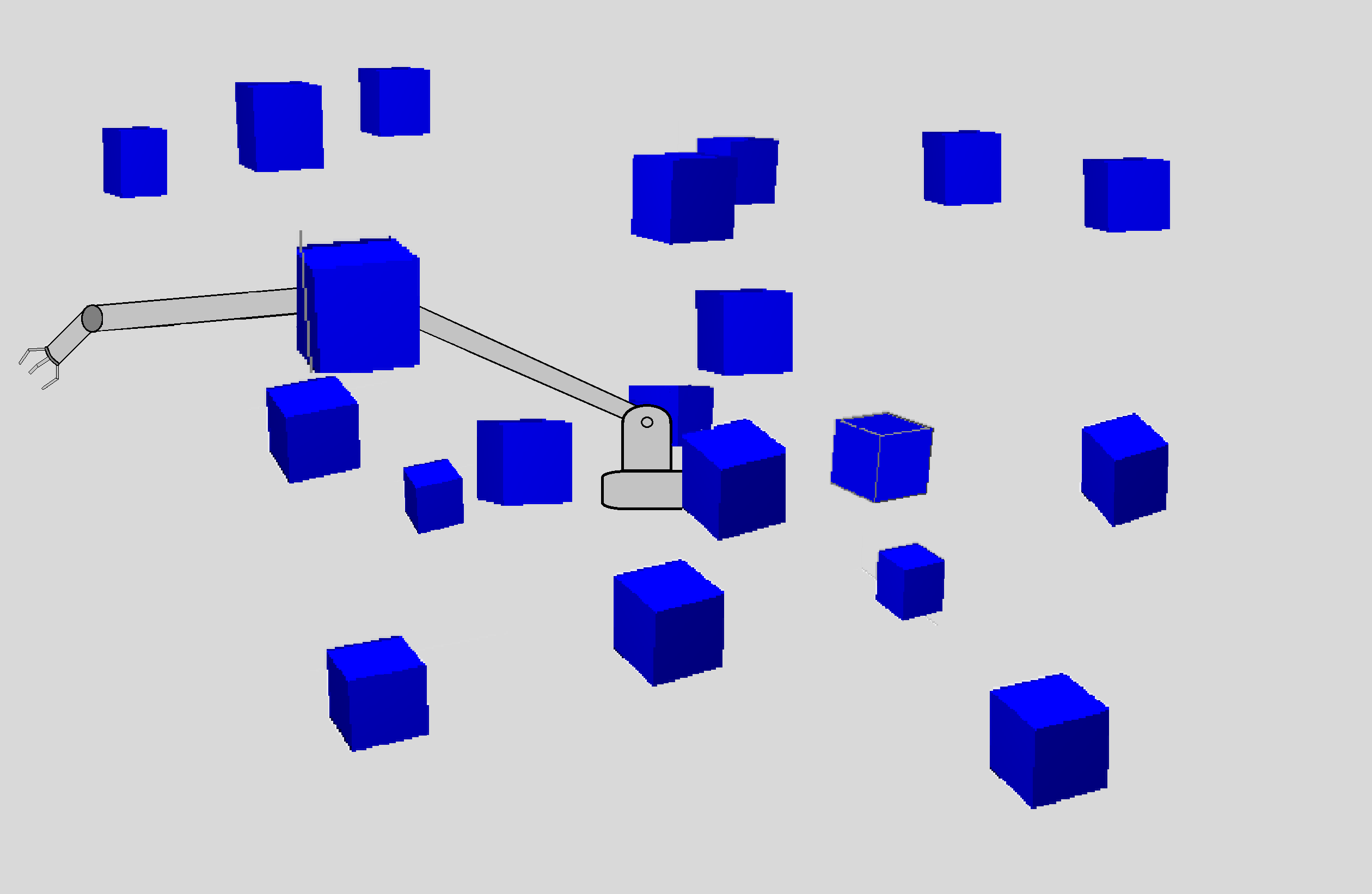
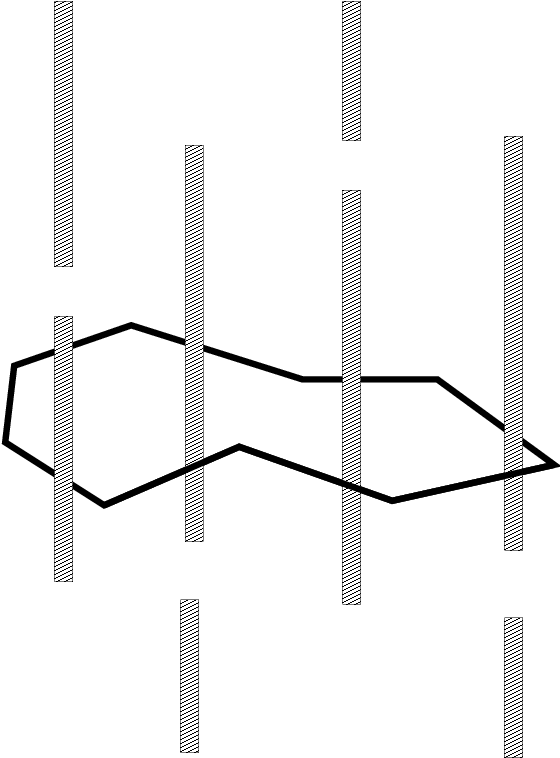
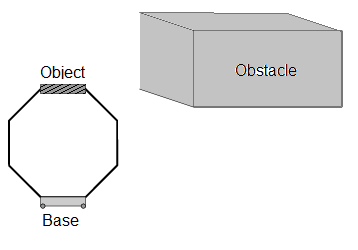
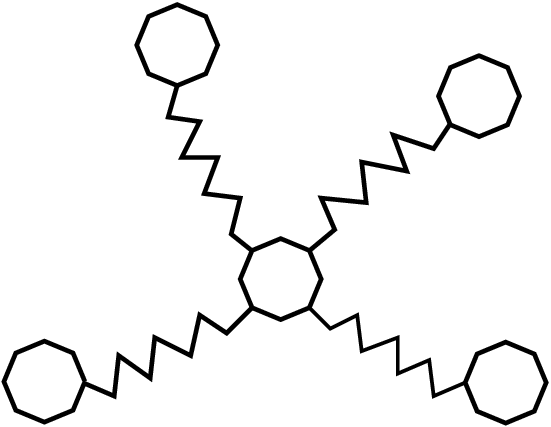
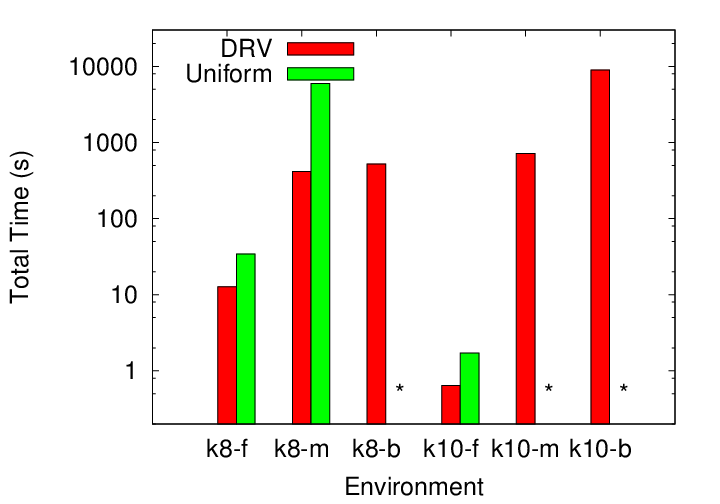
We allow each method to attempt 2000 samples. Reachable volume sampling may be slower than other methods, but it is more successfull in generating valid samples in unconstrained systems.
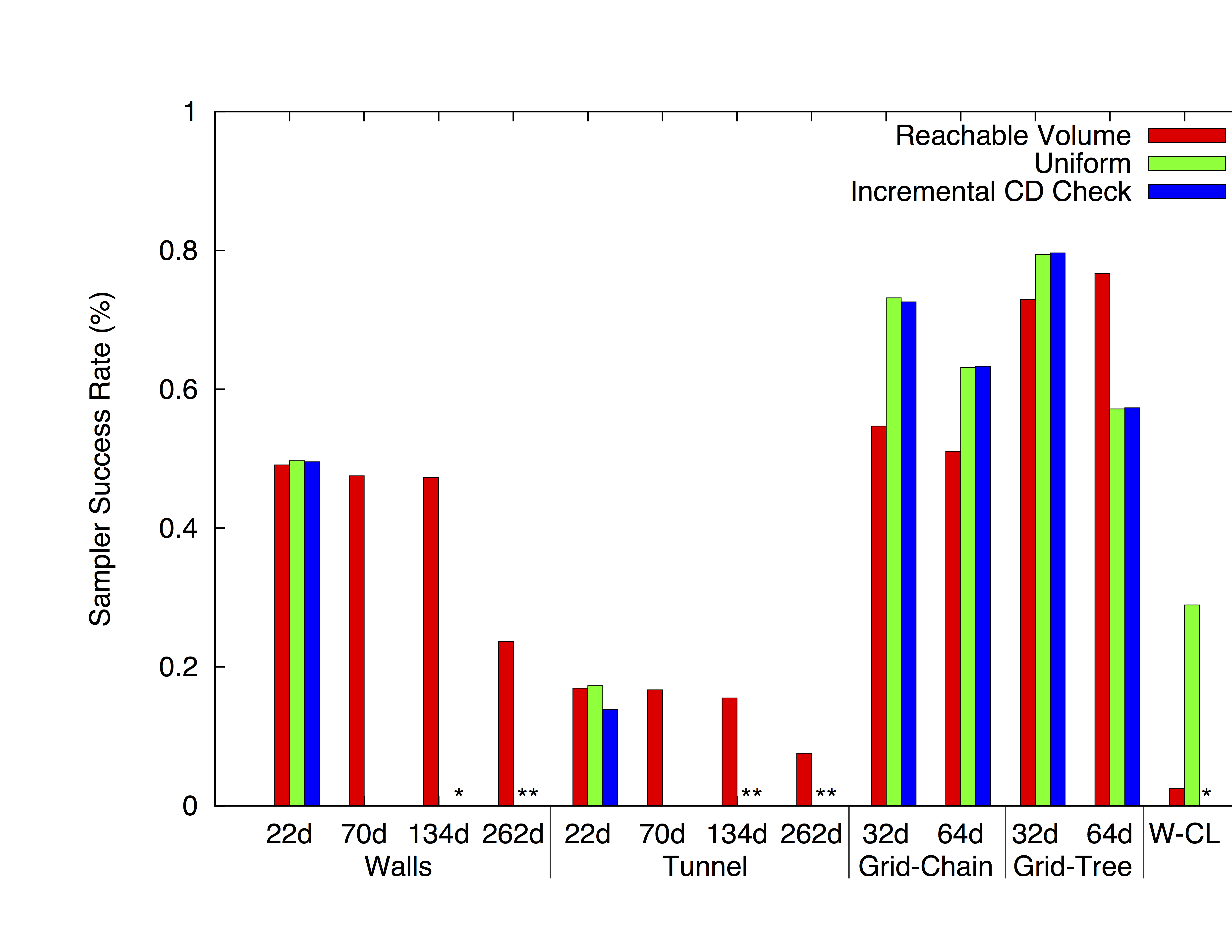
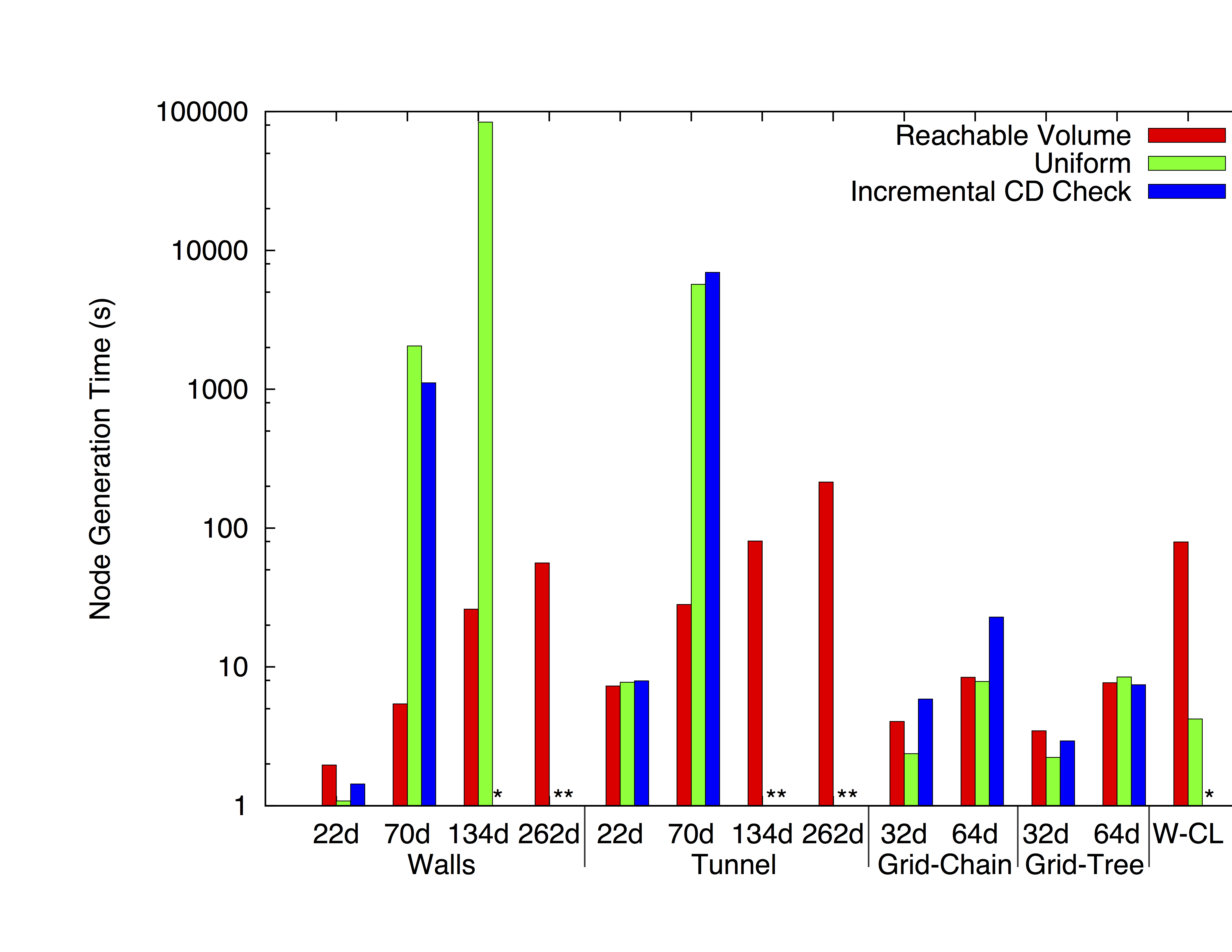
For constrained systems (e.g., closed chains), reachable volume sampling is often the only method able to generate samples in the allotted time (20 hours).
We also demonstrate different combionations of local planners and distance metrics in the context of PRM planning with reachable volume samples in the walls environment. We show both a 22 dof unconstrained chain (w-22) and a 22 dof closed chain (w-cc). We compare reachable volume local planning (rv) and straightline local planning (sl). For reachable volume local planning, we use either scaled Euclidean (se) or reachable volume distance (rv) for selecting the k nearest neighbors for connection.
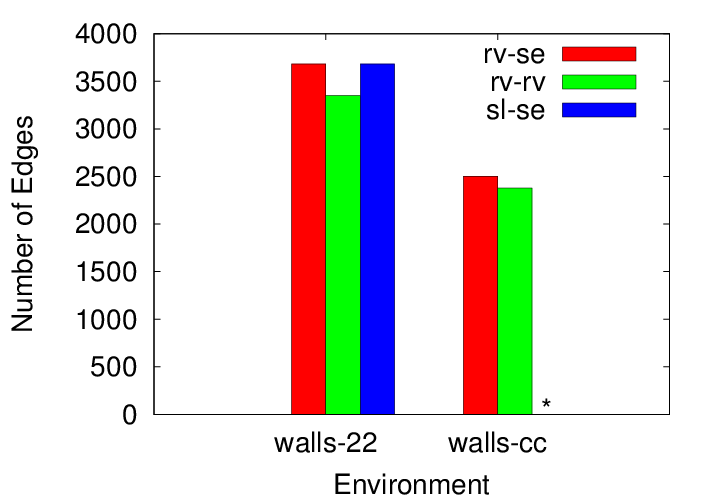
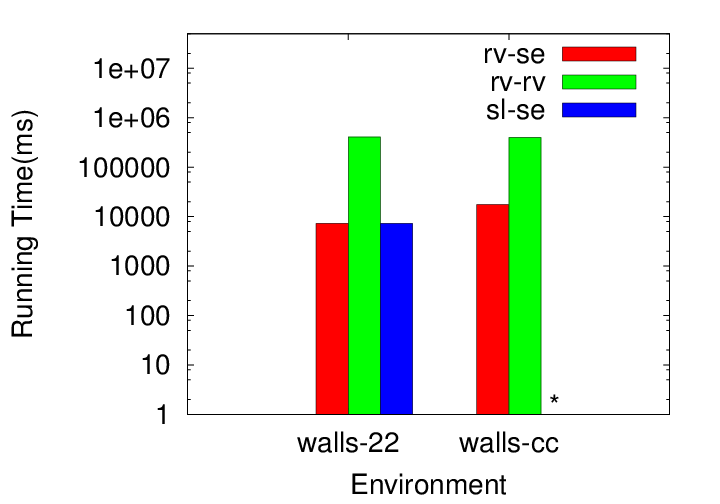
We present a novel method for stepping reachable volume samples to generate nearby samples that are also in their reachable volumes. We use this stepping method in an RV-Expand function to grow an RRT. It guarantees that the steps will satisfy constraints. It works by interatively stepping joints in RV-space and updating affected available reachable volumes:





This reachable volume RRT (RVRRT) can be applied to high dof problems that RRTs have previously been unable to solve. It can also be applied to constrained systems where it generates paths that are guaranteed to adhere to the problem's constraints.
Reachable Volume RRT in Practice
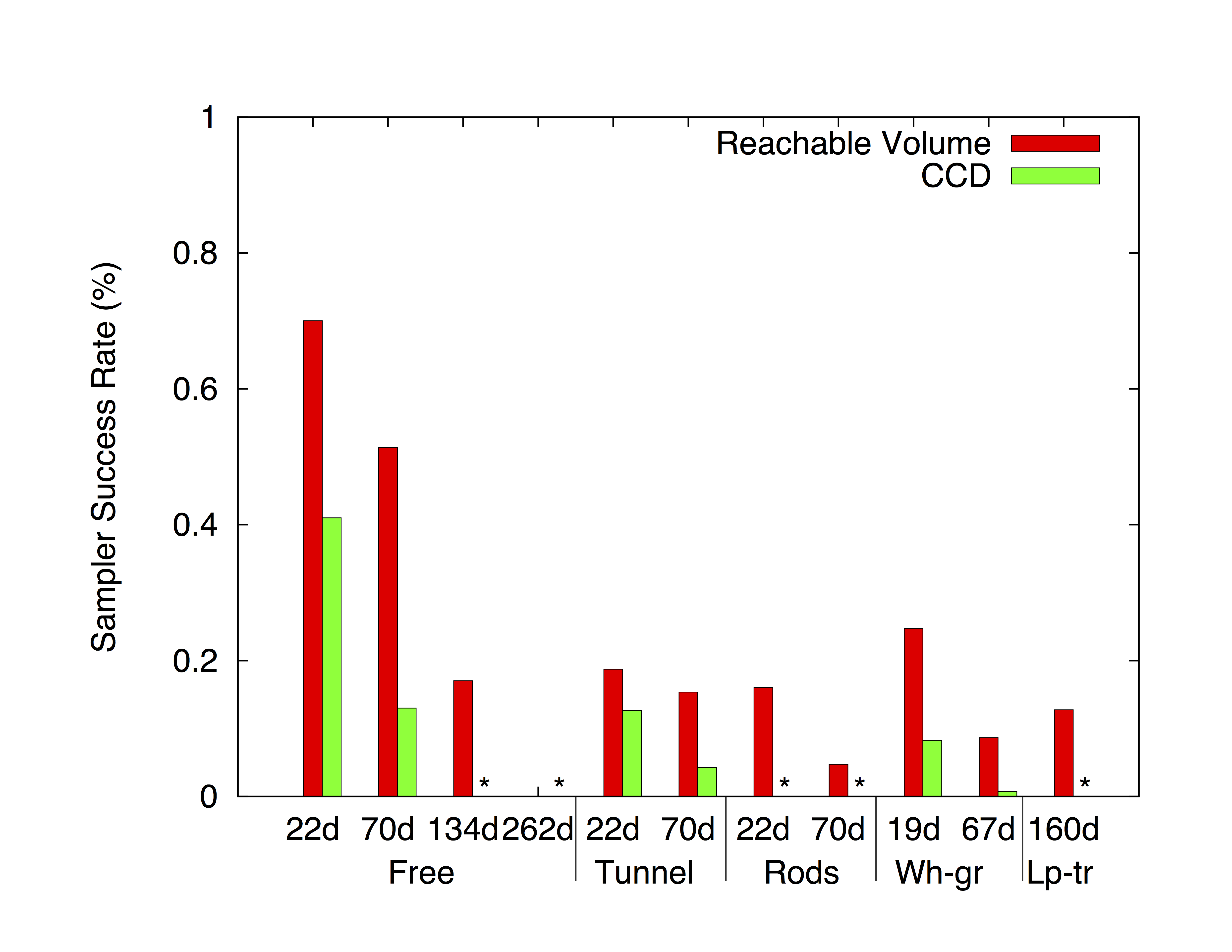
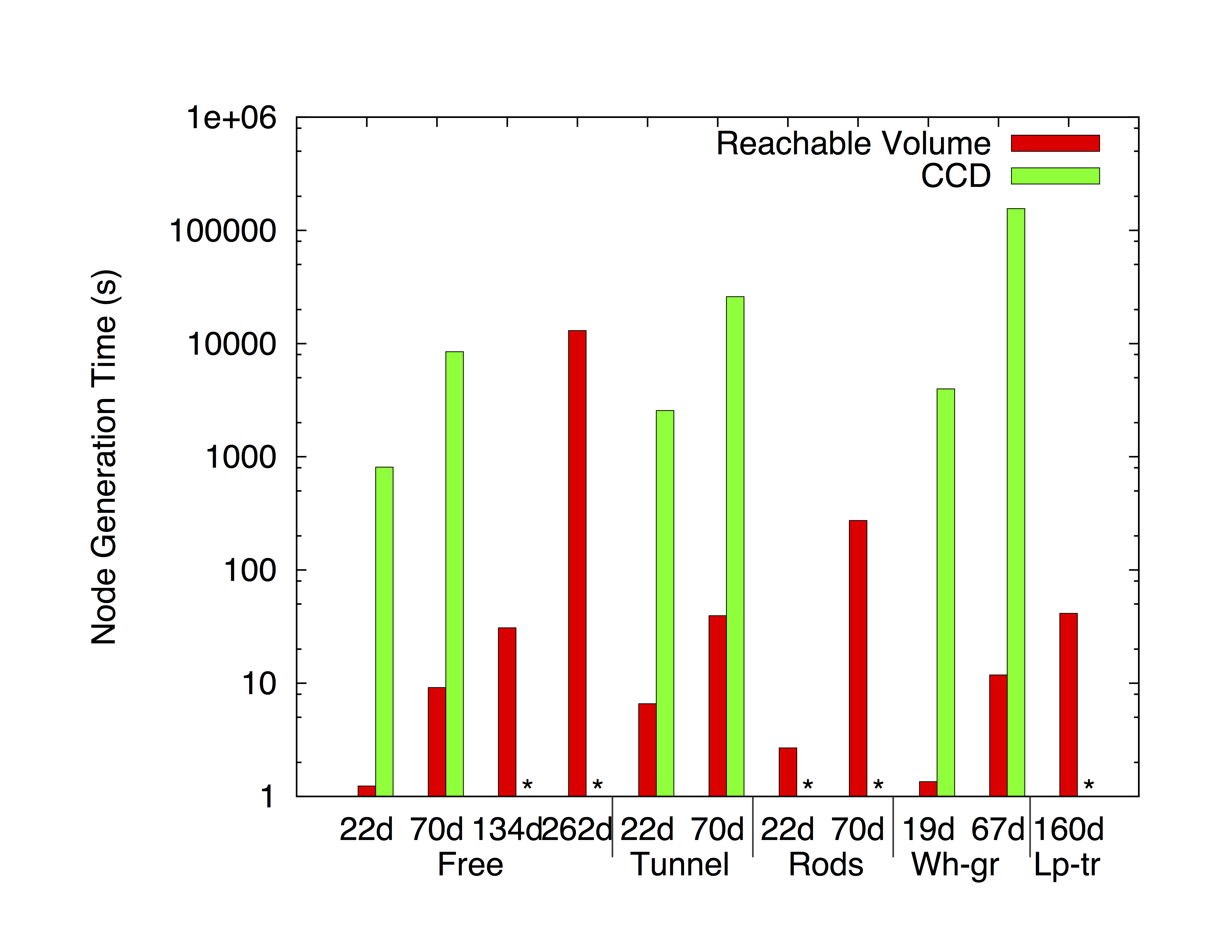
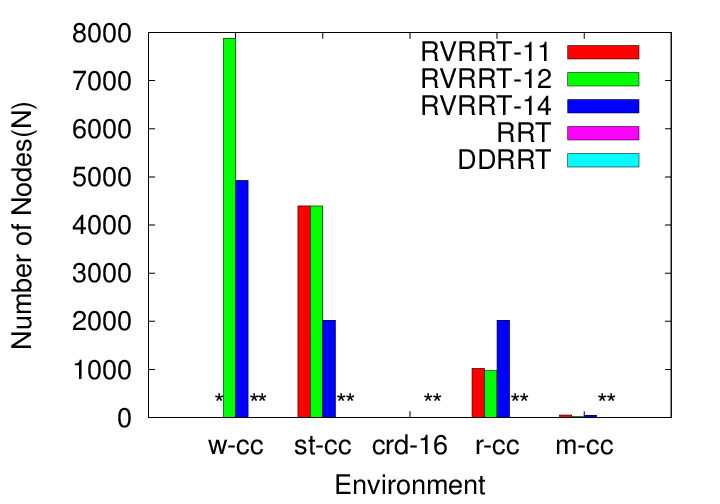
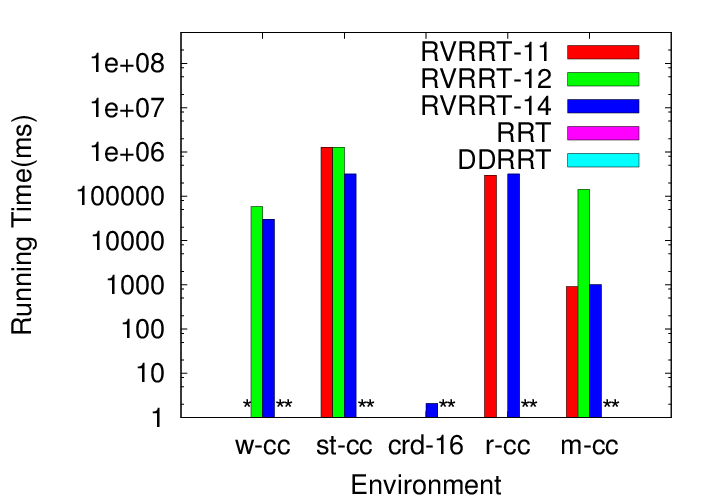
We consider a variety of environments and study robots with 22 to 134 dof:

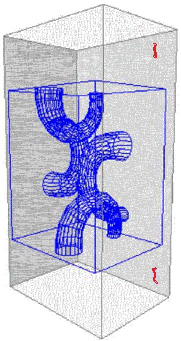
We compare RVRRT to RRT and DDRRT. The different variants of RVRRT correspond to differen input parameters (see our publications for more details). For unconstrained systems, RVRRTs require less computation time and fewer nodes to solve the query, and in some cases are capable of solving difficult problems that other methods cannot. (Each method was allowed to run a maximum of 8 hours). The running time of RVRRT is generally higher than RRT in low dof problems but comparable to RRT and DDRRT in higher dof problems.
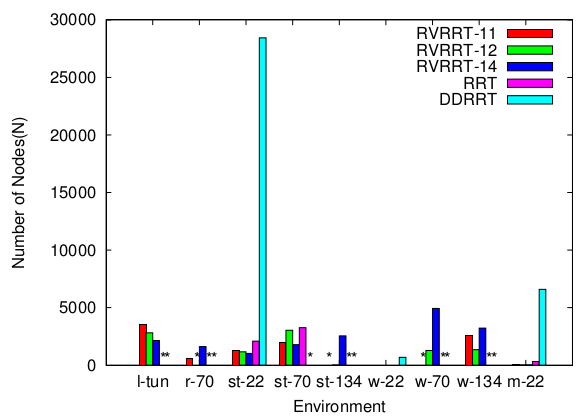
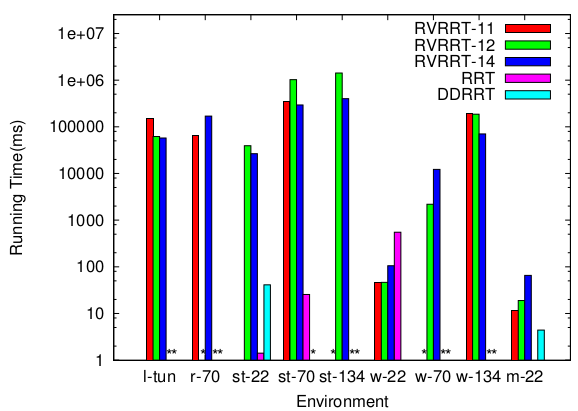
For constrained systems (e.g., closed chains), RVRRT is often the only method able to solve the problem.
DRV: Directed Reachable Volumes
Reachable volumes have been highly successful in solving constrained problems and problems with many degrees of freedom, but they cannot handle rotational joints. We develop directed reachable volumes (DRVs) which reparameterizes traditional configuration space into a new planning space called DRV-space. DRV-space makes planning the motion of a Fetch robot (composed of several revolute joints) to extract binders and place them in a bin feasible.
Rotational joints often appear in industrial robots because they weigh less and are more cost effective than spherical joints. Motion planning for manipulators with rotational joints is challenging because the actuation range for each link is constrained by the placement and orientation of other links.
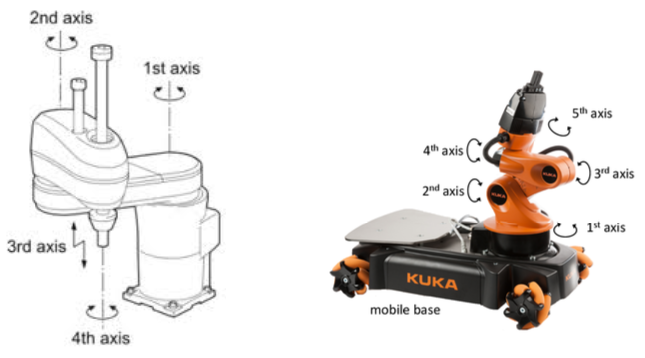
DRV-space encodes the oriented volume of workspace that individual joints can access in the context of how other joints are placed. DRVs extend the concept of reachable volumes (RVs) to handle rotational joints in addition to spherical and prismatic joints. DRVs are also able to handle constraints on the orientation as well as the position of a robot's joints and end-effectors. (RVs only handle positional constraints.)
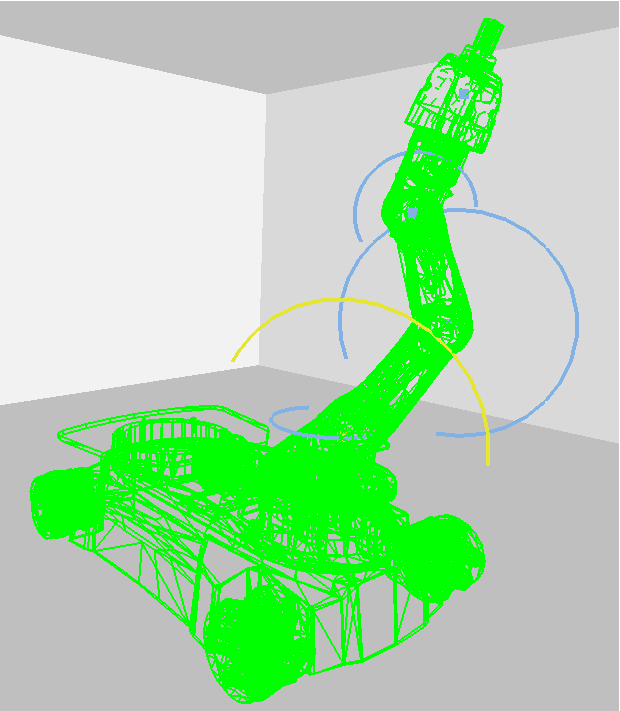
We demonstrate DRVs in the context of sampling based motion planning to solve pick-and-place problems with the KUKA Youbot. We study 2 different versions of the manipulator: the standard 5 dof arm (K8) and a 7 dof arm with 2 additional links (K10). We also vary the pick position from the front of the cubbard (f), the middle of the cubbard (m) and the back of the cubbard (b). DRVs are able to solve all variants while uniform random sampling cannot.
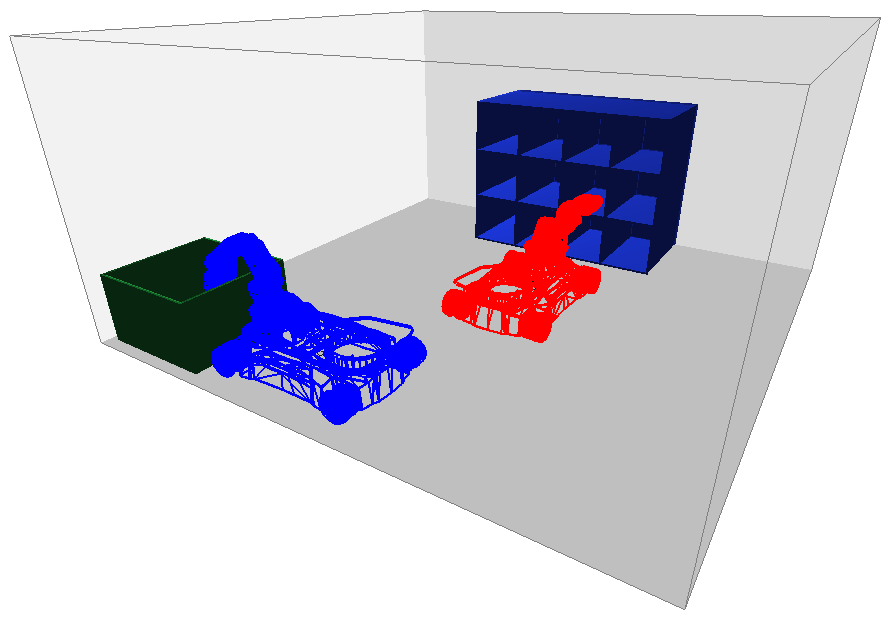
Motion planning for closed-chain systems is particularly difficult due to additional constraints, so-called closure constraints , placed on the system. In fact, the probability of randomly selecting a set of joint angles that satisfy the closure constraints is zero. Reachable distance sampling overcomes this challenge by precomputing the subspace where the closure constraints are satisfied and then directly sampling in this subspace. This method represents the chain as a hierarchy of sub-chains by recursively breaking down the problem into smaller subproblems. Each sub-chain in the hierarchy may be partitioned into other, smaller sub-chains forming a closed loop. For any sub-chain, we can compute the attainable distance (reachable distance or length) between its two endpoints recursively. Instead of randomly sampling in the joint angle space, we recursively sample in the reachable distance space. This provides distinct advantages over traditional approaches:
Our method can be used to significantly improve the performance of sampling-based planners for closed-chain systems such as Probabilistic Roadmap Methods (PRM) and Rapidly-Exploring Randomized Trees. We provide the necessary motion planning primitives (namely sampling and local planning) to implement most sampling-based motion planners. Our experimental results show that our method is fast and efficient in practice making sampling configurations with closure constraints comparable to sampling open chain configurations that ignore closure constraints entirely. It is easy to implement and general. It is also extends to more distance-related constraints besides the ones demonstrated here.
In our initial work, we proposed a two-stage kinematics-based probabilistic roadmap (KBPRM) planner for closed chains. In the first stage, we build a (small) kinematic roadmap that deals solely with the robot's kinematics and utilizes both forward and inverse kinematics in its construction. In the second stage, the environment is populated with copies of the kinematic roadmap, and rigid body connections are made between nodes with the same closure type. Both stages employ PRM planners to construct their roadmaps. Our experimental results indicate that the use of kinematics to guide the generation and connection of closure configurations is very beneficial, both reducing the computation costs and improving the connectivity of the resulting roadmap as compared to previous purely randomized approaches.
The efficiency of KBPRM depends critically on how the linkage is partitioned into open chains. The original method assumed the Partition was provided as input to the problem. In the extended work, we proposed a fully automated method for partitioning an arbitrary linkage into open chains and for determining which should be positioned using the inverse kinematic solver. Even so, the size (number of links) of the closed loops that can be handled by this method is limited because the inverse solver can only be applied to small chains. To handle high DOF closed loops, we show how we can use the Iterative Relaxation of Constraints (IRC) strategy to efficiently handle large loops while still only using inverse kinematics for small chains.
Sampling-based motion planning with reachable volumes for high-degree-of-freedom manipulators, Troy McMahon, Shawna Thomas, and Nancy M Amato, The International Journal of Robotics Research, Vol: 37, Issue: 7, pp. 779-817, Jun 2018. DOI: 10.1177/0278364918779555 @article{mcmahon2018sampling, Motion planning for constrained systems is a version of the motion planning problem in which the motion of a robot is limited by constraints. For example, one can require that a humanoid robot such as a PR2 remain upright by constraining its torso to be above its base or require that an object such as a bucket of water remain upright by constraining the vertices of the object to be parallel to the robotÃÂâÃÂÃÂÃÂÃÂs base. Grasping can be modeled by requiring that the end effectors of the robot be located at specified handle positions. Constraints might require that the robot remain in contact with a surface, or that certain joints of the robot remain in contact with each other (e.g., closed chains). Such problems are particularly difficult because the constraints form a manifold in C-space, and planning must be restricted to this manifold. High-degree-of-freedom motion planning and motion planning for constrained systems has applications in parallel robotics, grasping and manipulation, computational biology and molecular simulations, and animation. We introduce a new concept, reachable volumes, that are a geometric representation of the regions the joints and end effectors of a robot can reach, and use it to define a new planning space called RV-space where all points automatically satisfy a problemÃÂâÃÂÃÂÃÂÃÂs constraints. Visualizations of reachable volumes can enable operators to see the regions of workspace that different parts of the robot can reach. Samples and paths generated in RV-space naturally conform to constraints, making planning for constrained systems no more difficult than planning for unconstrained systems. Consequently, constrained motion planning problems that were previously difficult or unsolvable become manageable and in many cases trivial. We introduce tools and techniques to extend the state-of-the-art sampling-based motion planning algorithms to RV-space. We define a reachable volumes sampler, a reachable volumes local planner, and a reachable volumes distance metric. We showcase the effectiveness of RV-space by applying these tools to motion planning problems for robots with constraints on the end effectors and/or internal joints of the robot. We show that RV-based planners are more efficient than existing methods, particularly for higher-dimensional problems, solving problems with 1000 or more degrees of freedom for multi-loop and tree-like linkages.
Keywords: Manipulation Planning, Reachability Analysis, Sampling-Based Motion Planning
Links : [Published] BibTex
title={Sampling-based motion planning with reachable volumes for high-degree-of-freedom manipulators},
author={McMahon, Troy and Thomas, Shawna and Amato, Nancy M},
journal={The International Journal of Robotics Research},
volume={37},
number={7},
pages={779--817},
year={2018},
publisher={SAGE Publications Sage UK: London, England}
}Abstract
Manipulation Planning with Directed Reachable Volumes, Troy McMahon, Read Sandstrom, Shawna Thomas, Nancy M. Amato, Proc. IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), pp. 4026-4033, Vancouver, Canada, Sep 2017. DOI: 10.1109/IROS.2017.8206257 @inproceedings{mcmahon2017manipulation, Motion planning for manipulators with rotational joints is challenging because the actuation range for each link is constrained by the placement and orientation of other links. Thus, finding paths that avoid self-collision is non-trivial. However, rotational joints are often used in industrial robots. We develop a reparameterization of the planning problem called directed reachable volumes that provides an explicit representation of the workspace regions that the joints and end effectors can reach given the placement and orientation of other links. This formulation, while similar in spirit to prior reachable volume work, does not rely on the same restrictive assumptions that preclude prior work from handling rotational joints. We provide primitive planning operations that can be used in the context of state-of-the-art motion planning methods. We present experimental validation of directed reachable volumes by demonstrating a simulated pick-and-place scenario using realistic robots with rotational joints.
Keywords: Manipulation Planning, Reachability Analysis, Sampling-Based Motion Planning
Links : [Published] BibTex
title={Manipulation planning with directed reachable volumes},
author={McMahon, Troy and Sandstr{\"o}m, Read and Thomas, Shawna and Amato, Nancy M},
booktitle={2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS)},
pages={4026--4033},
year={2017},
organization={IEEE}
}Abstract
Sampling Based Motion Planning with Reachable Volumes, Troy McMahon, Doctoral dissertation, Texas A & M University, College Station, Texas, USA, Aug 2016. @phdthesis{mcmahon2016sampling, Motion planning for constrained systems is a version of the motion planning problem in which the motion of a robot is limited by constraints. For example, one can require that a humanoid robot such as a PR2 remain upright by constraining its torso to be above its base or require that an object such as a bucket of water remain upright by constraining the vertices of the object to be parallel to the robotÃÂÃÂÃÂÃÂÃÂÃÂÃÂâÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂs base. Grasping can be modeled by requiring that the end effectors of the robot be located at specified handle positions. Constraints might require that the robot remain in contact with a surface, or that certain joints of the robot remain in contact with each other (e.g., closed chains). Such problems are particularly difficult because the constraints form a manifold in C-space, and planning must be restricted to this manifold. High degree of freedom motion planning and motion planning for constrained systems has applications in parallel robotics, grasping and manipulation, computational biology and molecular simulations, and animation. In this work, we introduce a new concept, reachable volumes, that are a geometric representation of the regions the joints and end effectors of a robot can reach, and use it to define a new planning space, called RV-space, where all points automatically satisfy a problemÃÂÃÂÃÂÃÂÃÂÃÂÃÂâÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂs constraints. Visualizations of reachable volumes can enable operators to see the regions of workspace that different parts of the robot can reach. Samples and paths generated in RV-space naturally conform to constraints, making planning for constrained systems no more difficult than planning for unconstrained systems. Consequently, constrained motion planning problems that were previously difficult or unsolvable become manageable and in many cases trivial. We provide tools and techniques to extend the state of the art sampling based motion planning algorithms to RV-space. We define a reachable volume sampler, a reachable volume local planner and a reachable volume distance metric. We showcase the effectiveness of RV-space by applying these tools to motion planning problems for robots with constraints on the end effectors and/or internal joints of the robot. We show that RV-based planners are more efficient than existing methods, particularly for higher dimensional problems, solving problems with 1000+ degrees of freedom for multi-loop, and tree-like linkages.
Keywords: Manipulation Planning, Reachability Analysis, Sampling-Based Motion Planning
Links : [Published] BibTex
title={Sampling based motion planning with reachable volumes},
author={McMahon, Troy Anthony},
year={2016}
}Abstract
Reachable Volume RRT, Troy McMahon, Shawna L. Thomas, Nancy M. Amato, 2015 IEEE International Conference on Robotics and Automation (ICRA), pp. 2977-2984, Seattle, Washington, USA, May 2015. DOI: 10.1109/ICRA.2015.7139607 @INPROCEEDINGS{7139607, author={T. {McMahon} and S. {Thomas} and N. M. {Amato}}, booktitle={2015 IEEE International Conference on Robotics and Automation (ICRA)}, title={Reachable volume RRT}, year={2015}, volume={}, number={}, pages={2977-2984}, doi={10.1109/ICRA.2015.7139607}} Reachable volumes are a new technique that allows one to efficiently restrict sampling to feasible/reachable regions of the planning space even for high degree of freedom and highly constrained problems. However, they have so far only been applied to graph-based sampling-based planners. In this paper we develop the methodology to apply reachable volumes to tree-based planners such as Rapidly-Exploring Random Trees (RRTs). In particular, we propose a reachable volume RRT called RVRRT that can solve high degree of freedom problems and problems with constraints. To do so, we develop a reachable volume stepping function, a reachable volume expand function, and a distance metric based on these operations. We also present a reachable volume local planner to ensure that local paths satisfy constraints for methods such as PRMs. We show experimentally that RVRRTs can solve constrained problems with as many as 64 degrees of freedom and unconstrained problems with as many as 134 degrees of freedom. RVRRTs can solve problems more efficiently than existing methods, requiring fewer nodes and collision detection calls. We also show that it is capable of solving difficult problems that existing methods cannot.
Keywords: Manipulation Planning, Reachability Analysis, Sampling-Based Motion Planning
Links : [Published] BibTex
Abstract
Sampling Based Motion Planning with Reachable Volumes: Application to Manipulators and Closed Chain Systems, Troy McMahon, Shawna L. Thomas, Nancy M. Amato, 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 3705-3712, Chicago, Illinois, USA, Sep 2014. DOI: 10.1109/IROS.2014.6943082 @INPROCEEDINGS{6943082, author={T. {McMahon} and S. {Thomas} and N. M. {Amato}}, booktitle={2014 IEEE/RSJ International Conference on Intelligent Robots and Systems}, title={Sampling based motion planning with reachable volumes: Application to manipulators and closed chain systems}, year={2014}, volume={}, number={}, pages={3705-3712}, doi={10.1109/IROS.2014.6943082}} Reachable volumes are a geometric representation of the regions the joints of a robot can reach. They can be used to generate constraint satisfying samples for problems including complicated linkage robots (e.g. closed chains and graspers). They can also be used to assist robot operators and to help in robot design.We show that reachable volumes have an O(1) complexity in unconstrained problems as well as in many constrained problems. We also show that reachable volumes can be computed in linear time and that reachable volume samples can be generated in linear time in problems without constraints. We experimentally validate reachable volume sampling, both with and without constraints on end effectors and/or internal joints. We show that reachable volume samples are less likely to be invalid due to self-collisions, making reachable volume sampling significantly more efficient for higher dimensional problems. We also show that these samples are easier to connect than others, resulting in better connected roadmaps. We demonstrate that our method can be applied to 262-dof, multi-loop, and tree-like linkages including combinations of planar, prismatic and spherical joints. In contrast, existing methods either cannot be used for these problems or do not produce good quality solutions.
Keywords: Manipulation Planning, Reachability Analysis, Sampling-Based Motion Planning
Links : [Published] BibTex
Abstract
Sampling-Based Motion Planning with Reachable Volumes: Theoretical Foundations, Troy McMahon, Shawna Thomas, Nancy M. Amato, In Proc. IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, Jun 2014. DOI: 10.1109/ICRA.2014.6907820 @INPROCEEDINGS{6907820, author={T. {McMahon} and S. {Thomas} and N. M. {Amato}}, booktitle={2014 IEEE International Conference on Robotics and Automation (ICRA)}, title={Sampling-based motion planning with reachable volumes: Theoretical foundations}, year={2014}, volume={}, number={}, pages={6514-6521}, doi={10.1109/ICRA.2014.6907820}} We introduce a new concept, reachable volumes, that denotes the set of points that the end effector of a chain or linkage can reach. We show that the reachable volume of a chain is equivalent to the Minkowski sum of the reachable volumes of its links, and give an efficient method for computing reachable volumes. We present a method for generating configurations using reachable volumes that is applicable to various types of robots including open and closed chain robots, tree-like robots, and complex robots including both loops and branches. We also describe how to apply constraints (both on end effectors and internal joints) using reachable volumes. Unlike previous methods, reachable volumes work for spherical and prismatic joints as well as planar joints. Visualizations of reachable volumes can allow an operator to see what positions the robot can reach and can guide robot design. We present visualizations of reachable volumes for representative robots including closed chains and graspers as well as for examples with joint and end effector constraints.
Keywords: Manipulation Planning, Reachability Analysis, Sampling-Based Motion Planning
Links : [Published] BibTex
Abstract
Reachable distance space: Efficient sampling-based planning for spatially constrained systems, Xinyu Tang, Shawna Thomas, Phillip Coleman, Nancy M. Amato, The International Journal of Robotics Research, Vol: 29, Issue: 7, pp. 916-934, Jun 2010. DOI: 10.1177/0278364909357643 @article{tang2010reachable, Motion planning for spatially constrained robots is difficult due to additional constraints placed on the robot, such as closure constraints for closed chains or requirements on end-effector placement for articulated linkages. It is usually computationally too expensive to apply sampling-based planners to these problems since it is difficult to generate valid configurations. We overcome this challenge by redefining the robotâÂÂs degrees of freedom and constraints into a new set of parameters, called reachable distance space (RD-space), in which all configurations lie in the set of constraint-satisfying subspaces. This enables us to directly sample the constrained subspaces with complexity linear in the number of the robotâÂÂs degrees of freedom. In addition to supporting efficient sampling of configurations, we show that the RD-space formulation naturally supports planning and, in particular, we design a local planner suitable for use by sampling-based planners. We demonstrate the effectiveness and efficiency of our approach for several systems including closed chain planning with multiple loops, restricted end-effector sampling, and on-line planning for drawing/sculpting. We can sample single-loop closed chain systems with 1,000 links in time comparable to open chain sampling, and we can generate samples for 1,000-link multi-loop systems of varying topologies in less than a second.
Keywords: Motion Planning, Sampling-Based Motion Planning
Links : [Published] BibTex
title={Reachable distance space: Efficient sampling-based planning for spatially constrained systems},
author={Tang, Xinyu and Thomas, Shawna and Coleman, Phillip and Amato, Nancy M},
journal={The international journal of robotics research},
volume={29},
number={7},
pages={916--934},
year={2010},
publisher={SAGE Publications Sage UK: London, England}
}Abstract
Planning with Reachable Distances: Fast Enforcement of Closure Constraints, Xinyu Tang, Shawna Thomas, Nancy M. Amato, In Proc. IEEE International Conference on Robotics and Automation (ICRA), Roma, Italy, Apr 2007. DOI: 10.1109/ROBOT.2007.363872 @INPROCEEDINGS{4209490, author={X. {Tang} and S. {Thomas} and N. M. {Amato}}, booktitle={Proceedings 2007 IEEE International Conference on Robotics and Automation}, title={Planning with Reachable Distances: Fast Enforcement of Closure Constraints}, year={2007}, volume={}, number={}, pages={2694-2699}, doi={10.1109/ROBOT.2007.363872}} Motion planning for closed-chain systems is particularly difficult due to additional closure constraints placed on the system. In fact, the probability of randomly selecting a set of joint angles that satisfy the closure constraints is zero. We propose planning with reachable distance (PRD) to overcome this challenge by first precomputing the subspace satisfying the closure constraints, then directly sampling in it. To do so, we represent the chain as a hierarchy of sub-chains. Then we calculate the "closure" sub-space as appropriate reachable distance ranges of sub-chains satisfying the closure constraints. This provides two distinct advantages over traditional approaches: (1) configurations are quickly sampled and converted to joint angles using basic trigonometry functions instead of more expensive inverse kinematics solvers, and (2) configurations are guaranteed to be closed. In this paper, we describe this hierarchical chain representation and give a sampling algorithm with complexity linear in the number of links. We provide the necessary motion planning primitives for most sampling-based motion planners. Our experimental results show our method is fast, making sampling closed configurations comparable to sampling open chain configurations that ignore closure constraints. Our method is general, easy to implement, and also extends to other distance-related constraints besides the ones demonstrated here
Keywords: Manipulation Planning, Reachability Analysis, Sampling-Based Motion Planning
Links : [Published] BibTex
Abstract